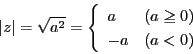次:: 複素平面
上: 複素数
前: 複素数
日本の高校教科書では次のように複素数が定義されている.
平方すると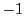 になる新しい数を一つ考えて,これを文字
になる新しい数を一つ考えて,これを文字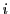 で表し,虚数単位とよぶ.すなわち
で表し,虚数単位とよぶ.すなわち
さらに,二つの実数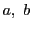 を用いて
を用いて
と表される数を考え,これを複素数という.
この定義は実は次のような疑問をもたせる.
- 「新しい数を一つ考えて」と言うが,勝手に考えて作っただけではないか.
- 実数
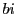 と
と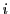 の積は定義されていない.
の積は定義されていない.
- また,
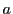 と
と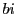 の和
の和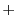 も定義されていない
も定義されていない
- 「平方すると
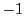 になる数」は
になる数」は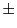 と二つあるはずなのに,どちらをとってもいいのか.
と二つあるはずなのに,どちらをとってもいいのか.
教科書では,これらの疑問には答えることなく,次のことが出てくる.
- 複素数の相等:
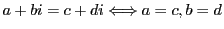
- 加減法
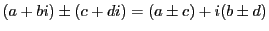 (複号同順)
(複号同順)
- 乗法
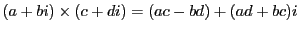
- 除法
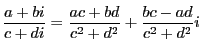
- 共役複素数:
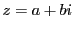 に対して,
に対して,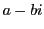 を
を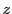 の共役複素数といい
の共役複素数といい
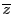 と記す.
と記す.
これで四則計算は実数と同じようにできるが,先の疑問点はそのままである.
この,教科書で作られた複素数の集合を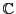 とする.
とする.
そこで,これまでに構成した実数をもとに,改めて複素数を構成しなおそう.
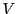 を2つの実数の組(順序は区別する)の集合とする.つまり,
を2つの実数の組(順序は区別する)の集合とする.つまり,
とする.
この集合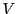 の要素の間の加法を次のように定める.
の要素の間の加法を次のように定める.
このとき,加法の単位元は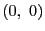 で
で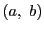 の加法に関する逆元は
の加法に関する逆元は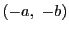 である.
である.
乗法を
と定める.これらの演算に関して,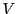 は公理
は公理![[*]](images/crossref.gif) を満たす.実際,
を満たす.実際,
- 加法:
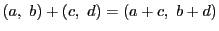
- 加法,乗法の交換法則,加法の結合法則は明かである.
- 乗法の結合法則:
より成立.
- 乗法の逆元:
より
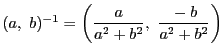 .
.
となる.つまり,この2つの演算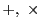 によって
によって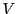 は体にある.
は体にある.
次にこの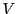 と
と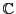 が体として同型であることは,次のように確認できる.
が体として同型であることは,次のように確認できる.
集合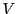 から複素数の集合
から複素数の集合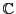 への写像
への写像
を
で定める.これは明らかに一対一写像である.
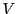 の演算の定義と
の演算の定義と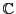 の計算法則から,加法や乗法の演算の結果も
の計算法則から,加法や乗法の演算の結果も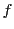 で対応する.
この対応の存在によって体として同型である.
で対応する.
この対応の存在によって体として同型である.
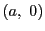 の形をした要素からなる
の形をした要素からなる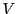 の部分集合は,この写像でちょうど
の部分集合は,この写像でちょうど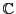 の部分集合である実数
の部分集合である実数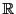 に対応する.
に対応する.
複素数の集合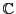 のモデルの構成法は一つではない.
のモデルの構成法は一つではない.
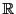 を今までどおり実数体とする. 実数係数の文字
を今までどおり実数体とする. 実数係数の文字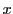 の多項式の全体を
の多項式の全体を
とする.明らかに![$R[x]$](images/img38.gif) は環
は環![[*]](images/crossref.gif) である.
である.![$R[x]$](images/img38.gif) を「実数体上の多項式環」という.
を「実数体上の多項式環」という.
そこで多項式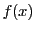 を多項式
を多項式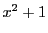 で割った余りを
で割った余りを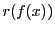 と書くことにし,
集合
と書くことにし,
集合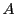 を
を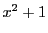 で割った余りの集合
で割った余りの集合
とする.例えば,
は次のように求められる.
割り算の余りなので
が成り立つ.
だから集合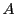 の四則演算を,多項式の四則演算そのもので定めれば,
の四則演算を,多項式の四則演算そのもので定めれば,
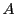 が環であることは自明である.
が環であることは自明である.
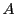 においては積の逆元が存在する.
任意の一次式
においては積の逆元が存在する.
任意の一次式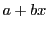 に対して
に対して
となる一次式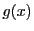 が存在する.実際,
求める
が存在する.実際,
求める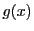 を
を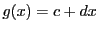 と置く.まず
と置く.まず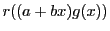 を求める.
を求める.
よって
とおく.これより
これから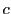 と
と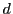 について解いて
について解いて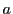 と
と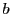 で表すと
で表すと
となる.つまり
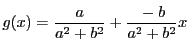 である.
である.
かくして には乗法に関する逆元が存在した.
には乗法に関する逆元が存在した. も体である.
も体である.
また実数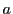 に対して
に対して
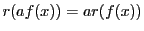 である.だから
である.だから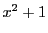 で割った余りとしての
で割った余りとしての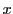 や1を
や1を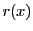 や
や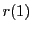 と書くと
と書くと
つまり
となる.そしてこれが体である.
この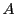 から
から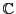 への写像
への写像
を
でさだめると,これが一対一写像でしかも演算の結果も対応する.
つまり同型を定める写像である.
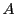 も複素数体と同型でそのモデルであるといえる.
も複素数体と同型でそのモデルであるといえる.
先に作った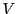 と今回の
と今回の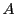 ももちろん体として同型である.つまり
ももちろん体として同型である.つまり
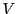 から
から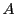 への写像
への写像
を
で定めればよい.
この対応で,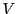 の要素と
の要素と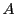 の要素は1対1に対応し,演算の結果も対応しているから,
同じ型である.
の要素は1対1に対応し,演算の結果も対応しているから,
同じ型である.
結局,教科書が定義しようとした複素数の集合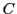 と,
同型となる2つのモデルがを,独立に構成できた.
2つのモデルとも,確かに存在している.
大切なことは,実数の演算を下に,あらたな体が定義できるということである.
と,
同型となる2つのモデルがを,独立に構成できた.
2つのモデルとも,確かに存在している.
大切なことは,実数の演算を下に,あらたな体が定義できるということである.
以下,この体をいずれも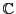 と記し,複素数体という.
と記し,複素数体という.
「みかん1個」と,「スプーン1本」などから数「1」が抽出されたように,
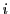 は
は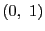 や
や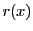 から抽出されたものを表す記号である.
それは勝手に作ったものではない.つまり
から抽出されたものを表す記号である.
それは勝手に作ったものではない.つまり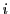 は
「平方すると
は
「平方すると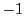 になる新しい数を一つ考え」たのではなく,
抽出されたものとして確かに存在している.
になる新しい数を一つ考え」たのではなく,
抽出されたものとして確かに存在している.
また,2次行列の部分集合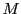 を次のように定める.
を次のように定める.
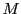 において加法,乗法は2次行列の加法,乗法をそのまま用いるとする.
において加法,乗法は2次行列の加法,乗法をそのまま用いるとする.
このとき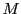 もまた可換体となり,
もまた可換体となり,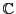 とが同型であることが示される.
とが同型であることが示される.
複素数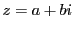 に対してその絶対値
に対してその絶対値
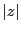 を
を
で定義する.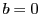 のとき
のとき
であるから,実数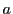 の絶対値と一致する.
の絶対値と一致する.
Subsections



次:: 複素平面
上: 複素数
前: 複素数
Aozora
2020-04-17
になる新しい数を一つ考えて,これを文字
で表し,虚数単位とよぶ.すなわち
を用いて
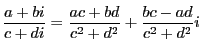
![]() を2つの実数の組(順序は区別する)の集合とする.つまり,
を2つの実数の組(順序は区別する)の集合とする.つまり,
![]() の要素の間の加法を次のように定める.
の要素の間の加法を次のように定める.
![[*]](images/crossref.gif) を満たす.実際,
を満たす.実際,
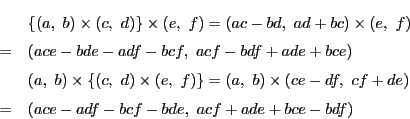
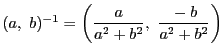 .
.
![]() と
と![]() が体として同型であることは,次のように確認できる.
が体として同型であることは,次のように確認できる.
![]() から複素数の集合
から複素数の集合![]() への写像
への写像
![]() の形をした要素からなる
の形をした要素からなる![]() の部分集合は,この写像でちょうど
の部分集合は,この写像でちょうど![]() の部分集合である実数
の部分集合である実数![]() に対応する.
に対応する.
![]() を今までどおり実数体とする. 実数係数の文字
を今までどおり実数体とする. 実数係数の文字![]() の多項式の全体を
の多項式の全体を
![[*]](images/crossref.gif) である.
である.![]() を多項式
を多項式![]() で割った余りを
で割った余りを![]() と書くことにし,
集合
と書くことにし,
集合![]() を
を![]() で割った余りの集合
で割った余りの集合
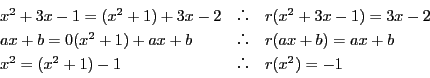
![]() においては積の逆元が存在する.
任意の一次式
においては積の逆元が存在する.
任意の一次式![]() に対して
に対して
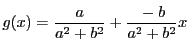 である.
である.
![]() には乗法に関する逆元が存在した.
には乗法に関する逆元が存在した.![]() も体である.
も体である.
![]() に対して
に対して
![]() である.だから
である.だから![]() で割った余りとしての
で割った余りとしての![]() や1を
や1を![]() や
や![]() と書くと
と書くと
![]() から
から![]() への写像
への写像
![]() と今回の
と今回の![]() ももちろん体として同型である.つまり
ももちろん体として同型である.つまり
![]() から
から![]() への写像
への写像
![]() と,
同型となる2つのモデルがを,独立に構成できた.
2つのモデルとも,確かに存在している.
大切なことは,実数の演算を下に,あらたな体が定義できるということである.
と,
同型となる2つのモデルがを,独立に構成できた.
2つのモデルとも,確かに存在している.
大切なことは,実数の演算を下に,あらたな体が定義できるということである.
![]() と記し,複素数体という.
と記し,複素数体という.
![]() は
は![]() や
や![]() から抽出されたものを表す記号である.
それは勝手に作ったものではない.つまり
から抽出されたものを表す記号である.
それは勝手に作ったものではない.つまり![]() は
「平方すると
は
「平方すると![]() になる新しい数を一つ考え」たのではなく,
抽出されたものとして確かに存在している.
になる新しい数を一つ考え」たのではなく,
抽出されたものとして確かに存在している.
![]() を次のように定める.
を次のように定める.
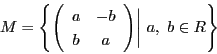
![]() もまた可換体となり,
もまた可換体となり,![]() とが同型であることが示される.
とが同型であることが示される.