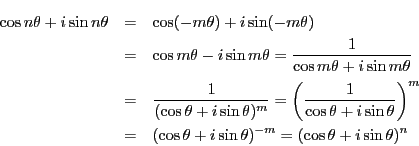次: 微分法
上: 複素数
前: 構成方法
複素数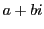 に直交座標平面の点
に直交座標平面の点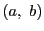 を対応させることにより,
複素数の集合
を対応させることにより,
複素数の集合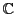 は平面上の点と一対一に対応する.
この対応が定められた平面を,複素平面という.
複素平面のうち実数に対応する部分を実軸,純虚数に対応する部分と0を虚軸という.
は平面上の点と一対一に対応する.
この対応が定められた平面を,複素平面という.
複素平面のうち実数に対応する部分を実軸,純虚数に対応する部分と0を虚軸という.
このとき,複素数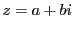 の絶対値
の絶対値
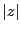 は,
直交座標平面での原点と点
は,
直交座標平面での原点と点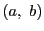 との距離に他ならない.
この距離に関して,複素平面は距離空間である.
との距離に他ならない.
この距離に関して,複素平面は距離空間である.
今後この定義によって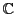 を複素平面と同一視する.
を複素平面と同一視する.
平面座標に極座標がある.つまり 直交座標で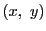 となる点が極座標では
となる点が極座標では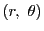 であるとする.
2つの座標の間には
であるとする.
2つの座標の間には
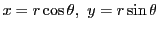 が成り立つ.
が成り立つ.
これに応じて,複素数は極形式という表し方がある.
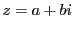 のとき
のとき
「形式」というのは「形」でのことで,同じ複素数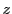 が,
が,
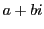 と
と
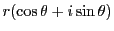 という2つの形をもつ.
極座標の
という2つの形をもつ.
極座標の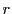 は任意の実数でよいのだが,極形式のときには,
は任意の実数でよいのだが,極形式のときには,
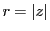 にとり,負にはしないようにするのが約束である.
また,角
にとり,負にはしないようにするのが約束である.
また,角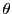 は
は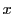 軸の正の方向から反時計回りに計る.
角
軸の正の方向から反時計回りに計る.
角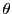 は偏角とよばれ
は偏角とよばれ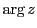 と書く.
と書く.
このとき,三角関数の加法定理によって偏角の和と複素数の積が対応する.
とすると
これから同様にして
これから.
等が成り立ち,対数関数と同じ等式になる.
後に述べるように,複素関数としての等式
が成り立ち,逆にここから三角関数の加法定理が帰結する.
次定理もまた,ここからただちに示されるが,
ここでは,実の三角関数の定理として証明しておく.
定理 1 (ド・モアブルの定理)
任意の整数
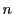
に対して
が成り立つ.
■
証明
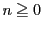 のとき.数学的帰納法で示す.
のとき.数学的帰納法で示す.
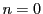 のときは両辺1であるから成立する.
のときは両辺1であるから成立する.
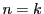 で成立するとして,
で成立するとして,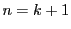 で成立することを示す.
で成立することを示す.
よって,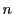 が負でないときは示された.
が負でないときは示された.
次に,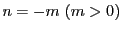 のとき
のとき
よって,この場合も成立し,題意は示された.□
Subsections
Aozora
2020-04-17
![]() の絶対値
の絶対値
![]() は,
直交座標平面での原点と点
は,
直交座標平面での原点と点![]() との距離に他ならない.
この距離に関して,複素平面は距離空間である.
との距離に他ならない.
この距離に関して,複素平面は距離空間である.
![]() を複素平面と同一視する.
を複素平面と同一視する.
![]() のとき
のとき
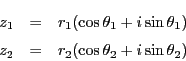
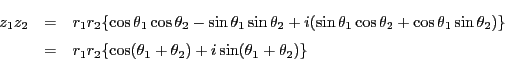
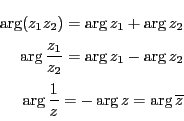
![]() のとき.数学的帰納法で示す.
のとき.数学的帰納法で示す.
![]() のときは両辺1であるから成立する.
のときは両辺1であるから成立する.
![]() で成立するとして,
で成立するとして,![]() で成立することを示す.
で成立することを示す.
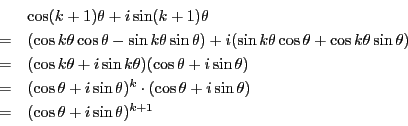
![]() のとき
のとき