連続とはいうまでもなく「つながっている」ということである.この世界が連続であるかどうか,それはわからない.物質に最小の単位があるのであれば,それが素粒子であれ,より小さいものであれ,その単位以上には分解できないのだから,棒を二つに切るのに任意のところできるというわけにはいかないことになる.切断に関して棒が連続であるとはいえない.
移動という観点から見れば,あそこからここまで不連続に移動したとは考えられないように思われる.途中を飛ばして移動できるとは思われないからだ.しかしこれも連続な座標系が,連続な時間とともに固定されていることを前提にするからいえるのである.もし時間が不連続なら,移動が連続であることに意味はない.
このように連続という概念は,考えれば考えるほど難しい.連続について深く考えようとする人は『無限と連続』(遠山啓,岩波新書)のような書をぜひとも読んでみてほしい.
数学では現実世界の連続性に関する思弁的な議論はしない.数学の対象としての連続なものを準備し,それを用いてこの世界を近似してつかむということだ.準備された連続なものを用いて現実を近似するのである.普通は![]() を有理数
を有理数![]() で近似するという.実は実数を準備しそれを用いてこの世界を連続な世界として近似するのだ.近似する側の実数は,そのために何が要請されるのか.
で近似するという.実は実数を準備しそれを用いてこの世界を連続な世界として近似するのだ.近似する側の実数は,そのために何が要請されるのか.
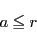
ここでさらに,上界が存在することを上に有界という.
上界に最小値が存在すれば,それを![]() の上限といい
の上限といい![]() と表す.
と表す.
同様に,
下界が存在することを下に有界という.
下界に最大値が存在すれば,それを![]() の下限といい
の下限といい![]() と表す.
と表す.
一方,有理数は連続の公理を満たさない.それは次の例でに示される.
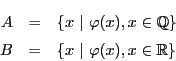
もし![]() が存在したとしそれを
が存在したとしそれを![]() とする.
とする.
![]() は,
は,![]() ,または
,または![]() であるようなすべての有理数
であるようなすべての有理数![]() に対し
に対し
![]() となるなかで最小の数である.
となるなかで最小の数である.
![]() も
も![]() なので
なので![]() である.
である.
ここで![]() とする.自然数
とする.自然数![]() に対して
に対して
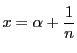 は
は
よって![]() である.
次に
である.
次に![]() とする.
とする.
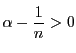 となる
となる
正の有理数![]() が
が![]() を満たせば
を満たせば
 となり両辺正なので
となり両辺正なので
 である.これは
である.これは![]() の最小性に反する.
の最小性に反する.
よって![]() である.ところがこれを満たす有理数は存在しないことは整数の範囲で証明される.つまり
である.ところがこれを満たす有理数は存在しないことは整数の範囲で証明される.つまり![]() に
に![]() は存在しない.
は存在しない.
ここで用いた「![]() を大きくすれば
を大きくすれば![]() がいくらでも小さくなる」ことは
がいくらでも小さくなる」ことは![]() におけるアルキメデスの原則から導かれる.それは後で明確にする.
におけるアルキメデスの原則から導かれる.それは後で明確にする.
実数の公理によって![]() の中で
の中で![]() の上限は存在する.それを
の上限は存在する.それを![]() とすると同様の考察で
とすると同様の考察で![]() となる数であり,この数のことを
となる数であり,この数のことを![]() と記するのだった.
と記するのだった.
実数![]() これが基礎である.
まずこの定義からただちに導かれるアルキメデスの原則を証明しよう.
これが基礎である.
まずこの定義からただちに導かれるアルキメデスの原則を証明しよう.
どのような公理系を採用するかで,この命題の位置づけが変わる.しかし,どのような公理系を採用しようと,そのなかで成立することが要請される.つまり公理系をどのようにするのかということよりも一般的な命題である.それでここでは『解析概論』の言葉を使う.
証明 背理法で示す.命題の否定は
任意の自然数![]() に対して
に対して![]() も自然数であるから
も自然数であるから![]() .ゆえに
.ゆえに
実際,任意の正の二つの有理数
![]() に関して
に関して
 となる自然数
となる自然数![]() が存在することは
が存在することは
アルキメデスの原則と,基本数列の収束,つまり完備性とあわせることで,実数の公理と同等になること,ここに二つの構成方法の同等性がある.
アルキメデスの時代は,もちろん座標の方法もないし,関数を式に表すことも知られていない.彼は放物線で囲まれた図形の面積を次のように求めた.一応座標に入れて説明する.アルキメデスはもっと図形的にやった.
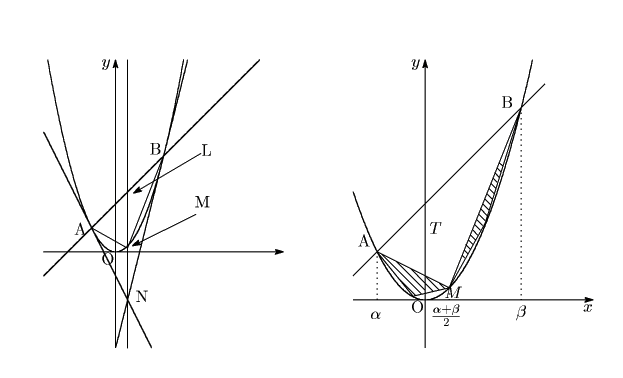
![]() 上の点
上の点
![]() ,
,
![]() をとる.
線分
をとる.
線分![]() と放物線で囲まれた図形の面積を
と放物線で囲まれた図形の面積を![]() としよう.
としよう.
![]() 座標が
座標が![]() と
と![]() の
の![]() 座標の中点と一致する点を
座標の中点と一致する点を![]() ,
,
![]() と
と![]() での接線の交点を
での接線の交点を![]() とする.このとき一般に
とする.このとき一般に
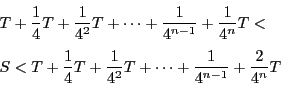
![]() なので,不等式は正の定数
なので,不等式は正の定数![]() を用いて
を用いて
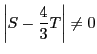 であるとしよう.
不等式は任意の
であるとしよう.
不等式は任意の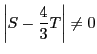 であるかぎり
であるかぎり
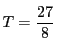 だから
だから
1.![]() ,
,![]() ,
,![]() のいずれか一つに定まる.
のいずれか一つに定まる.
2.![]() かつ
かつ![]() ならば,
ならば,![]() である.
である.
ただし,
![]() の最大の元とは,
の最大の元とは,
![]() で任意の
で任意の![]() の元
の元![]() に対して
に対して![]() または
または![]() が成り立つものをいう.
■
が成り立つものをいう.
■
自然数,整数,有理数は人間が数として考えるものであり,その公理とは,これらの数の構造を公理として定式化したものである.数の存在は,現実の人間の数にかかわる生活のなかにあると言うこともできる.数学的には,集合の公理6.の無限公理は,まさに自然数の存在を一般化して公理としたものである.
それに対して,実数は理論からの要請ではないだろうか.であるなら,高校解析の基礎を築くという立場からは,有理数体![]() を出発点として実数が構成できることを示すことが基本である.
を出発点として実数が構成できることを示すことが基本である.
もちろん,一般の順序体で考え,実数の公理から導かれるいくつかの定理の相互関係を解明することも重要な問題なのであり,それは後に触れる.
実数の公理を満たすモデルを二つの方法で構成しよう.
実数モデルの一つの作り方はカントールによる.それは数列を用いる.したがってまず数列に関して必要なことを準備しなければならない.