

 次: 切断の方法
上: 実数の構成
前: 連続の公理
次: 切断の方法
上: 実数の構成
前: 連続の公理
整数,自然数,あるいは自然数と0の集合などから他の数学的対象への写像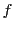 を数列という.ここでは,自然数の集合,あるいは自然数と0の集合から実数への写像を考える.自然数
を数列という.ここでは,自然数の集合,あるいは自然数と0の集合から実数への写像を考える.自然数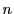 に対する値
に対する値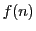 を
を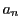 のように表し一般項という.
のように表し一般項という.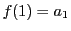 を初項という.
を初項という.
数列 が数
が数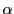 に収束することは,高校数学では
「
に収束することは,高校数学では
「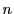 がかぎりなく大きくなるとき,
がかぎりなく大きくなるとき,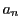 は
は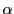 にかぎりなく近づく」と理解し,
にかぎりなく近づく」と理解し,
と書き表す.だが「かぎりなく」というのはどういうことだろうか.これは必ずしも明確ではない.また,「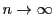 」は「
」は「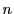 がいくらでも大きくなる」と理解する.しかし「いくらでも大きくなる」もまた必ずしも明確ではない.
がいくらでも大きくなる」と理解する.しかし「いくらでも大きくなる」もまた必ずしも明確ではない.
収束や極限値という概念の定義のなかの言葉にはこのような「無限」が潜んでいる.無限という概念は,人間にとって魅力あるものだが,集合論で見たように危険も伴う.収束や極限値を定義する言葉のなかに「無限」が現れることを避けることはできないのか.
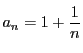 で定まる数列
で定まる数列 を考えよう.これは1に収束する.収束するということは,
を考えよう.これは1に収束する.収束するということは,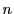 を大きくすれば
を大きくすれば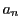 がいくらでも1に近くなるということだ.「いくらでも」ということは,どんな小さい正の実数
がいくらでも1に近くなるということだ.「いくらでも」ということは,どんな小さい正の実数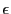 が指定されても,
が指定されても,
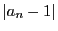 が
が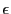 より小さくなるように
より小さくなるように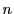 を大きくできるということではないか.1と
を大きくできるということではないか.1と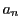 を
を
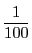 よりもっと近づけよ,といわれれば
よりもっと近づけよ,といわれれば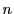 を100より大きくとればよい.
を100より大きくとればよい.
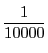 より小さくしたければ10000より大きくとればよい.「どんなに小さい」というが「小さい」ことは関係ない.「何が指定されても」ということだ.
より小さくしたければ10000より大きくとればよい.「どんなに小さい」というが「小さい」ことは関係ない.「何が指定されても」ということだ.
任意の正の実数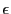 対し,
対し,
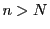 なら
なら
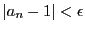 となる
となる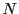 が存在する.
が存在する.
この命題のなかには「かぎりなく」や「いくらでも」という言葉はない.これをもって収束の定義としてはどうだろうか.
定義 10 (数列の収束)
数列

と数
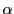
がある.
任意の正の実数
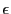
に対し,番号
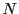
で
となるものが存在するとき,数列

は
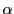
に収束するという.
■
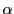 のことを極限値といい.
のことを極限値といい.
と書く.
「任意の正の実数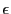 に対して,番号
に対して,番号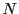 で…となるものが存在」というところは「どのような小さい」正の実数
で…となるものが存在」というところは「どのような小さい」正の実数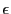 が指定されても,それに対して「つねに」番号
が指定されても,それに対して「つねに」番号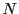 が存在する,ということを意味している.だが数学ではそのような副詞は必要ない.
が存在する,ということを意味している.だが数学ではそのような副詞は必要ない.
数列の極限に関し今後必要なことをいくつか示していこう.上記の論法を用いると.これを厳密に論証することができる.
定理 9
数列

および数列
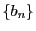
が収束して,
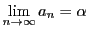
,
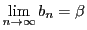
のとき,
が成り立つ.
■
証明
- (1)
-
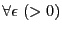 に対し自然数
に対し自然数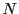 が存在して,
が存在して,
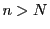 なら
なら
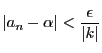 となる.このとき
となる.このとき
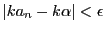 なので,
なので,
- (2)
-
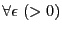 に対し自然数
に対し自然数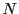 が存在して,
が存在して,
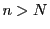 なら
なら
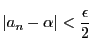 ,
,
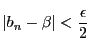 となる.このとき
となる.このとき
なので,
- (3)
- 数列
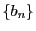 は収束するので,
は収束するので,
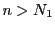 なら
なら
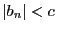 となる
正定数
となる
正定数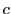 と自然数
と自然数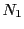 が存在する.
が存在する.
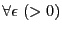 に対し自然数
に対し自然数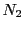 が存在して,
が存在して,
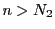 なら
なら
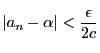 ,
,
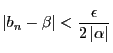 となる.
となる.
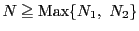 とすると,
とすると,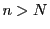 のとき
のとき
- (4)
-
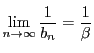 を示せば,(3)と併せて(4)は成立する.
を示せば,(3)と併せて(4)は成立する.
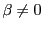 なので
なので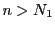 なら
なら
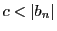 となる
となる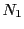 と正定数
と正定数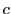 が存在する.
つまり
が存在する.
つまり
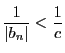 である.
である.
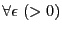 に対して
に対して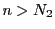 なら
なら
となる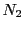 が存在する.
が存在する.
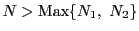 にとる.
にとる.
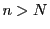 なら
なら
□
定理 10 (はさみうちの原理)
三つの数列
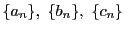
の各項の間に
がなり立ち,かつ数列

および数列
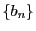
が同じ値
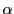
に収束するとする.
このとき,数列
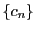
も収束し,極限値は
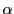
である.
■
証明
任意の正の実数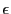 に対して
に対して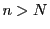 ならば
ならば
となる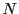 が存在する.このとき
が存在する.このとき
よって数列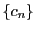 収束し,極限は
収束し,極限は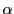 である.
□
である.
□
カントールは,以上の準備の下,基本数列を定義し,そのある同値類の集合として実数を定義した.
定義 11 (基本数列)
数列

が性質
をもつとき,これを
基本数列または
コーシー数列という.
■
集合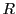 を有理数からなる基本数列
を有理数からなる基本数列 の集合とする.
の集合とする.
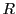 に属する二つの基本数列
に属する二つの基本数列
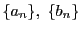 において
において
が成り立つとき,二つの基本数列
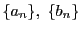 には関係〜が成り立つとする.
関係〜は同値関係である.
には関係〜が成り立つとする.
関係〜は同値関係である.
-
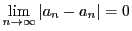 より,
より,
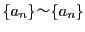 .
.
-
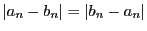 より
より
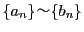 なら
なら
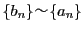 .
.
-
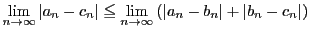 より
より
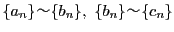 なら
なら
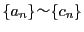 .
.
したがってこの関係〜による商集合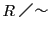 が定義される.数列
が定義される.数列 の属する同値類を
の属する同値類を
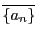 のように表そう.
のように表そう.
この商集合はまだ単に数列の同値類の集合でしかない.まずこれを順序体にしなければならない.次の手順でなされる.以下方針のみとし証明は略する.
- 和と積を
で定義する.
類の代表のとり方によらず定まる(これを"well-defined"という).
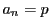 のような定数数列を
のような定数数列を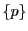 のように表すことにする.
加法の単位元は
のように表すことにする.
加法の単位元は
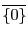 ,
乗法の単位元は
,
乗法の単位元は
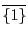 であり,このときそれぞれ逆元は
であり,このときそれぞれ逆元は
となる.ただし
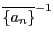 を考えるときは,
数列
を考えるときは,
数列 は0には収束しないときであり,
は0には収束しないときであり,
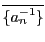 においては0の項を除いた
部分列を改めて数列
においては0の項を除いた
部分列を改めて数列 とすることにする.
とすることにする.
これによって四則演算が定義され,商集合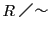 は体となること,
つまり実数の公理のI)が満たされる.
有理数
は体となること,
つまり実数の公理のI)が満たされる.
有理数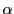 を数列
を数列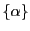 の
属する類と同一視することで
の
属する類と同一視することで
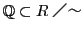 とできる.
とできる.
- 順序を次のように定義する.
この定義がwell-definedであることも示される.
このように定義された順序は順序の公理を満たす.
実数の公理II)が成り立つことがわかった.
つまり商集合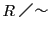 は順序体である.
は順序体である.
以下はこの順序体を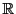 で表し,
で表し,
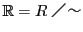 の要素を
の要素を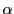 のように一文字で表す.
のように一文字で表す.
証明
アルキメデスの原則を満たさないということは,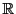 に埋め込まれた自然数の集合
に埋め込まれた自然数の集合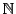 が上に有界であることを意味する.したがって,任意の
が上に有界であることを意味する.したがって,任意の
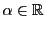 に対して
に対して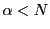 となる自然数
となる自然数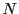 が存在すること,いいかえれば
が存在すること,いいかえれば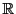 のなかで
のなかで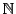 が有界でないことを示せばよい.
が有界でないことを示せばよい.
そこで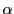 を定義する基本数列
を定義する基本数列 をとる.これは有界であるから
をとる.これは有界であるから
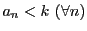 となる有理数
となる有理数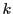 が存在する.ところが有理数体
が存在する.ところが有理数体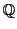 はアルキメデスの原則を満たすので,
はアルキメデスの原則を満たすので,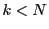 となる自然数
となる自然数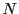 が存在する.つまり
が存在する.つまり
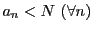 これは
これは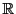 のなかに埋め込まれた
のなかに埋め込まれた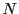 について
について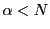 となることを意味しており,
となることを意味しており,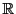 のなかで
のなかで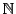 が有界でないこと示された.
□
が有界でないこと示された.
□
最後に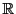 が実数の公理を満たすことを示す.
が実数の公理を満たすことを示す.
定理 12
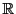
は連続性の公理を満たす.つまり,

を
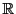
の空でない部分集合とする.集合

が上に有界ならば

の上限
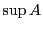
が存在する.
■
証明
上限の存在を示すために,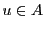 を適当にとり,
を適当にとり,
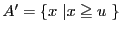 として
として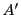 に上限が存在することを示せばよい.したがってはじめから
に上限が存在することを示せばよい.したがってはじめから は下にも有界であるとする.
は下にも有界であるとする.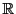 がアルキメデスの原則を満たすことは示されているので,
がアルキメデスの原則を満たすことは示されているので,
![$A\subset [a,\ b]$](images/img500.gif) となる有理数
となる有理数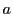 と
と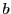 が存在する.
が存在する.
ここで の上限を構成する.閉区間の列
の上限を構成する.閉区間の列![$[a_n,\ b_n]$](images/img501.gif) で次の性質をもつものを定める.
で次の性質をもつものを定める.
- (i)
-
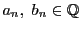 .
.
- (ii)
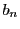 は
は の上界.
の上界.
- (iii)
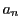 は
は の上界ではない.
の上界ではない.
これを次のように帰納的に定める.
- 1.
-
![$[a_0,\ b_0]=[a,\ b]$](images/img504.gif) .これは条件を満たす.
.これは条件を満たす.
- 2.
![$[a_n,\ b_n]$](images/img501.gif) は条件を満たすとする.
は条件を満たすとする.
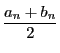 が
が の上界なら
の上界なら
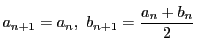 ,
,
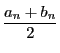 が
が の上界ではないなら
の上界ではないなら
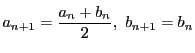 と定義する.
と定義する.
この
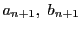 は(i)〜(iii)を満たしている.
は(i)〜(iii)を満たしている.
数列 は基本数列である. 実際,
は基本数列である. 実際,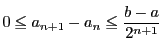 であるから
任意の正整数
であるから
任意の正整数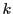 に対して
に対して
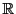 がアルキメデスの原則を満たすので
がアルキメデスの原則を満たすので
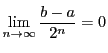 である.
したがって数列
である.
したがって数列 は基本数列である.
は基本数列である.
数列 の属する類,つまり
の属する類,つまり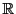 の要素を
の要素を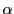 とする.
とする.
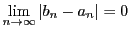 であるから,
数列
であるから,
数列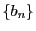 も同じ類に入る.
も同じ類に入る.
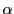 は
は の上限である.
の上限である.
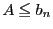 なので
なので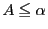 である.一方,任意の
である.一方,任意の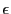 に対して
に対して
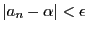 ,つまり
,つまり
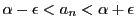 となる
となる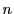 が存在する.
が存在する.
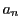 は上界ではないので
は上界ではないので
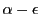 は上界ではない.
これは
は上界ではない.
これは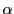 が
が の上限であることを意味している.
□
の上限であることを意味している.
□
このようにして実数の公理をすべて満たす集合が構成できたのである.したがって,この実数を用いて自然現象や社会現象を連続なものとして近似的につかみ,その解析をすることが保障されたのである.
この構成法によって,次の完備性が示される.
実数においてはこの逆もなり立つのである.
定理 13
実数からなる数列が収束するための必要十分条件は,
数列が基本数列であることである.
■
証明
まず収束数列は基本数列であることを確認しよう.
数列 が
が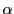 に収束するとする.任意の正の実数
に収束するとする.任意の正の実数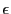 に対して
に対して
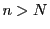 なら
なら
となる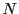 がある.
がある.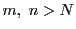 のとき
のとき
となる.よって数列 は基本数列である.
は基本数列である.
逆を示す.数列 が基本数列であるとする.
実数1に対し,
が基本数列であるとする.
実数1に対し,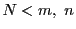 なら
なら
となる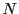 が存在する.
が存在する.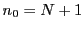 とする.
とする.
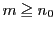 なら
なら
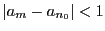 がなり立つので
がなり立つので
となり,すべての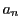 について
について
がなり立つ.つまり数列 は有界である.
は有界である.
集合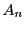 を
を
とする.実数の部分集合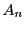 は有界なので上限と下限が存在する.
は有界なので上限と下限が存在する.
とおく.集合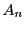 の要素は
の要素は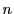 が増加すれば減少するので,
数列
が増加すれば減少するので,
数列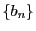 は単調増加,数列
は単調増加,数列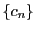 は単調減少である.
よって数列
は単調減少である.
よって数列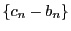 は単調減少である.
は単調減少である.
一方,数列 は基本数列なので,任意の
は基本数列なので,任意の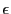 に対して,
に対して,
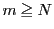 なら
なら
となる.これから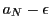 と
と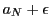 は集合
は集合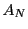 の下界と上界である.
したがって
の下界と上界である.
したがって
よって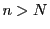 なら
なら
つまり
区間縮小法の原理(定理18)によって
数列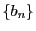 と数列
と数列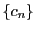 は同じ値
は同じ値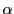 に収束する.
に収束する.
なので,数列 も
も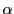 に収束する.
□
に収束する.
□
実数の集合においては,収束数列であることと,それが基本数列であることが同値である.有理数の集合においては同値ではない.これが同値であるという実数の集合の性質を完備性という.


 次: 切断の方法
上: 実数の構成
前: 連続の公理
次: 切断の方法
上: 実数の構成
前: 連続の公理
2014-05-23
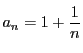 で定まる数列
で定まる数列![]() を考えよう.これは1に収束する.収束するということは,
を考えよう.これは1に収束する.収束するということは,![]() を大きくすれば
を大きくすれば![]() がいくらでも1に近くなるということだ.「いくらでも」ということは,どんな小さい正の実数
がいくらでも1に近くなるということだ.「いくらでも」ということは,どんな小さい正の実数![]() が指定されても,
が指定されても,
![]() が
が![]() より小さくなるように
より小さくなるように![]() を大きくできるということではないか.1と
を大きくできるということではないか.1と![]() を
を
![]() よりもっと近づけよ,といわれれば
よりもっと近づけよ,といわれれば![]() を100より大きくとればよい.
を100より大きくとればよい.
![]() より小さくしたければ10000より大きくとればよい.「どんなに小さい」というが「小さい」ことは関係ない.「何が指定されても」ということだ.
より小さくしたければ10000より大きくとればよい.「どんなに小さい」というが「小さい」ことは関係ない.「何が指定されても」ということだ.
対し,
なら
となる
が存在する.
 と数
と数 は
は![]() のことを極限値といい.
のことを極限値といい.
![]() に対して,番号
に対して,番号![]() で…となるものが存在」というところは「どのような小さい」正の実数
で…となるものが存在」というところは「どのような小さい」正の実数![]() が指定されても,それに対して「つねに」番号
が指定されても,それに対して「つねに」番号![]() が存在する,ということを意味している.だが数学ではそのような副詞は必要ない.
が存在する,ということを意味している.だが数学ではそのような副詞は必要ない.
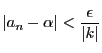 となる.このとき
となる.このとき
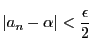 ,
,
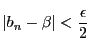 となる.このとき
となる.このとき
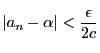 ,
,
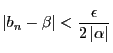 となる.
となる.
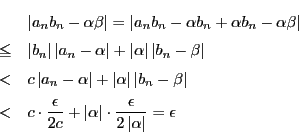
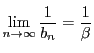 を示せば,(3)と併せて(4)は成立する.
を示せば,(3)と併せて(4)は成立する.
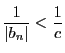 である.
である.
![]() に対して
に対して![]() なら
なら
 および数列
および数列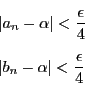
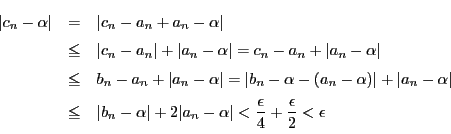
 が性質
が性質
![]() を有理数からなる基本数列
を有理数からなる基本数列 の集合とする.
の集合とする.
![]() に属する二つの基本数列
に属する二つの基本数列
![]() において
において
![]() のような定数数列を
のような定数数列を![]() のように表すことにする.
加法の単位元は
のように表すことにする.
加法の単位元は
![]() ,
乗法の単位元は
,
乗法の単位元は
![]() であり,このときそれぞれ逆元は
であり,このときそれぞれ逆元は
![]() は体となること,
つまり実数の公理のI)が満たされる.
有理数
は体となること,
つまり実数の公理のI)が満たされる.
有理数![]() を数列
を数列![]() の
属する類と同一視することで
の
属する類と同一視することで
![]() とできる.
とできる.
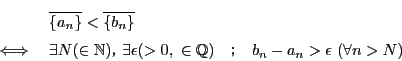
![]() は順序体である.
は順序体である.
![]() を定義する基本数列
を定義する基本数列 をとる.これは有界であるから
をとる.これは有界であるから
![]() となる有理数
となる有理数![]() が存在する.ところが有理数体
が存在する.ところが有理数体![]() はアルキメデスの原則を満たすので,
はアルキメデスの原則を満たすので,![]() となる自然数
となる自然数![]() が存在する.つまり
が存在する.つまり
![]() これは
これは![]() のなかに埋め込まれた
のなかに埋め込まれた![]() について
について![]() となることを意味しており,
となることを意味しており,![]() のなかで
のなかで![]() が有界でないこと示された.
□
が有界でないこと示された.
□
![]() が実数の公理を満たすことを示す.
が実数の公理を満たすことを示す.![]() の上限を構成する.閉区間の列
の上限を構成する.閉区間の列![]() で次の性質をもつものを定める.
で次の性質をもつものを定める.
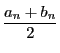 が
が![]() の上界なら
の上界なら
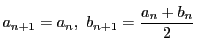 ,
,
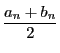 が
が![]() の上界ではないなら
の上界ではないなら
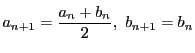 と定義する.
と定義する.
 は基本数列である. 実際,
は基本数列である. 実際,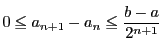 であるから
任意の正整数
であるから
任意の正整数![]() に対して
に対して
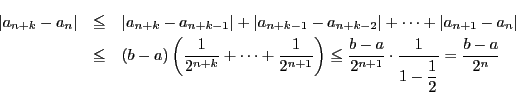
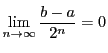 である.
したがって数列
である.
したがって数列![]() の属する類,つまり
の属する類,つまり![]() の要素を
の要素を![]() とする.
とする.
![]() であるから,
数列
であるから,
数列![]() も同じ類に入る.
も同じ類に入る.
![]() は
は![]() の上限である.
の上限である.
![]() なので
なので![]() である.一方,任意の
である.一方,任意の![]() に対して
に対して
![]() ,つまり
,つまり
![]() となる
となる![]() が存在する.
が存在する.
![]() は上界ではないので
は上界ではないので
![]() は上界ではない.
これは
は上界ではない.
これは![]() が
が![]() の上限であることを意味している.
□
の上限であることを意味している.
□
![]() が基本数列であるとする.
実数1に対し,
が基本数列であるとする.
実数1に対し,![]() なら
なら
![]() を
を
 は基本数列なので,任意の
は基本数列なので,任意の![]() に対して,
に対して,
![]() なら
なら
 も
も