

 次: 微分の方法
上: 関数の概念
前: 一様連続
次: 微分の方法
上: 関数の概念
前: 一様連続
定点から1の長さにある点の集合を単位円という.
その円周は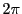 といわれる.ところで円周とは何なのか?
そもそも曲線の長さとはどのように定めるのか.
積分の定義の後で曲線の長さを定義する.それが定義35である.
といわれる.ところで円周とは何なのか?
そもそも曲線の長さとはどのように定めるのか.
積分の定義の後で曲線の長さを定義する.それが定義35である.
円とは1点からの距離が一定であるような点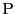 の集合である.
曲線の長さの定義にもとづいて円周もまた定義される.
半径1の時の円周の長さを
の集合である.
曲線の長さの定義にもとづいて円周もまた定義される.
半径1の時の円周の長さを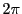 と定める.
と定める.
円の場合,円に内接する多角形の周囲の長さも決まる.
また円に外接する多角形の周囲の長さも決まる.
となる.
円弧の長さも,
その2点を結び円弧に内接する多角形の部分の周の長さの上限と,
その2点を結び円弧に外接する多角形の部分の周の長さの下限が一致すれるので,
これを円弧の長さと定めることができる.
これらは定義35とその後の関連定理で示される.そこでの論証では,
以下で円周を用いて定義される三角関数が使われることはない.したがって論理が循環することはない.
円周の長さ,この長さが確定した.
では角をどのように定めるのか.これは高校数学に登場する.
単位円周上の2点A,Bに対する円弧の長さをAからBへ左回りのとき正,
右回りのとき負とする.円弧は左回りを正,右回りを負とすれば何回でも回れるので,弧長は任意の実数値をとる.
そこで,弧長が となる円弧に対し,その中心角を
となる円弧に対し,その中心角を
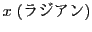 と定めるのである.弧度法による角は任意の実数値をとる.
と定めるのである.弧度法による角は任意の実数値をとる.
定義 18 (正弦関数,余弦関数)
直交座標平面に原点を中心として単位円をえがく.
円弧状の1点
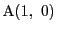
を固定し
他の点Pをとる.円弧APの長さが

,つまり
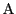
から
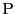
への中心角を

とし,
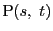
とする.
このとき,実数

の関数を
で定める.
■
分母が0にならないとき
でそれぞれの関数を定める.
このとき
が成り立つ.
三角関数については次の2点が基本である.
定理 32
- (1)
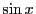 ,
,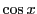 は実数全体で一様連続である.
は実数全体で一様連続である.
- (2)
-
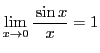 である.
■
である.
■
証明
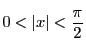 のとき,
のとき,
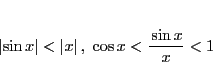 |
(1) |
が成り立つ.これを示す.
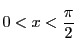 のとき.
点
のとき.
点  を中心とする半径1の円において,
中心角
を中心とする半径1の円において,
中心角  の扇形
の扇形  を考える.点
を考える.点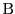 から
から
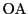 に垂線
に垂線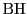 を引く.
点
を引く.
点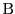 において円に接線
において円に接線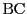 を引く.
円弧の長さが内接多角形の長さの上限であり,
外接多角形の長さの下限であったので
を引く.
円弧の長さが内接多角形の長さの上限であり,
外接多角形の長さの下限であったので
である.これから
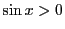 なので各辺を
なので各辺を 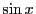 で割り逆数をとると,
で割り逆数をとると,
が得られる.
 が負のとき,
が負のとき, 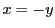 とおくと
とおくと
より同様の関係が成り立つ.これをもとに定理を示す.
-
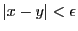 のとき.
のとき.
より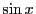 は一様連続.
は一様連続.
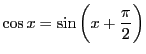 より
より
より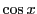 も一様連続である.
も一様連続である.
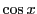 の連続性から
の連続性から
であるから不等式1より
である.
注意 3.1
日本の高校数学では,不等式
1を円の面積から導く.しかし,面積を求めるときに使った三角関数の微分・積分そのものはどのようにして導かれたのか,と考えると定理
1の極限(2) を基本的に用いて三角関数の微分をしていることに気づく.とするとここには循環論法が潜んでいる.
逆三角関数
三角関数は周期関数である.一般に周期関数の逆関数は多価関数になる.そこで周期関数の逆関数を考えるときは,まず周期関数の定義域を一価関数となるように制限し,その上で逆関数をとることが多い.多くの場合次のようにとる.
この区間で
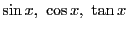 はそれぞれ単調増加,単調減少,単調増加で連続である.したがってこの値域を
はそれぞれ単調増加,単調減少,単調増加で連続である.したがってこの値域を![$[-1,\ 1]$](images/img942.gif) を定義域とする逆関数が定まる.それを
を定義域とする逆関数が定まる.それを
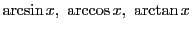 で表す.
このように主値を限定した逆関数を
で表す.
このように主値を限定した逆関数を
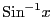 ,
,
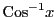 ,
,
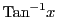 のように表すことも多い.
のように表すことも多い.
注意 3.2
![$[-1,\ 1]$](images/img942.gif)
の

に対して
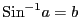
,
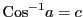
とおく.ただし,
![$b\in \left[-\dfrac{\pi}{2},\ \dfrac{\pi}{2}\right]$](images/img950.gif)
,
![$c\in \left[0,\ \pi\right]$](images/img951.gif)
である.
このとき
なので
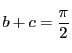
.つまり一般に
が成り立つ.
これは後に
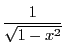
の原始関数を考える
とき(例
5.3)に意味をもつ.
自然対数の底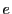 は本来は
は本来は
で定める.そして
を示す.
ところがこの方式では数列
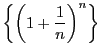 の収束や,
また
の収束や,
また
を示すのが簡単でないということで,
最近の日本高校でははじめから
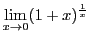 の極限を収束性の証明なしに定義に用いている.
本来の定義に立ちかえり,実数の連続性をもとに自然対数の底を定義しよう.
の極限を収束性の証明なしに定義に用いている.
本来の定義に立ちかえり,実数の連続性をもとに自然対数の底を定義しよう.
証明
数列 が単調増加で有界であることを示せばよい.
が単調増加で有界であることを示せばよい.

この極限値を自然対数の底といい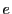 と表す.
と表す.
区間縮小法を用いる別証明も重要である.
先の証明のように二項定理を用いても出来るのだが,いろいろ役立つ便利な補題を紹介しよう.
補題 2
任意の自然数

と相異なる正数
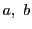
に関して不等式
が成り立つ.
■
証明
両辺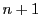 乗すれば補題が得られる.
□
乗すれば補題が得られる.
□
定理33の別証明
補題を
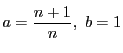 で用いると,
で用いると,
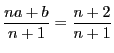 なので,
なので,
これは数列
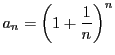 が単調増加であること示している.
が単調増加であること示している.
次に
補題を
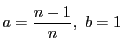 で用いると,
で用いると,
逆数をとって
これは数列
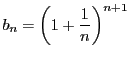 が単調減少であること示している.
また
が単調減少であること示している.
また
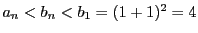 なので
なので
より
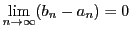 である.
したがって区間
である.
したがって区間
![$I_n=[a_n,\ b_n]$](images/img705.gif) に区間縮小法を適用すると,2つの数列
に区間縮小法を適用すると,2つの数列
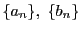 は同一の極限に収束することがわかる.
□
は同一の極限に収束することがわかる.
□
これで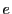 の値もある程度計算できる.
の値もある程度計算できる.
証明
ここで分母が1に収束することを示す.
であるから
□
証明
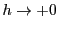 のときは
のときは
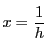 とおく.
とおく.
を示せばよい.
となる ,つまり
,つまり![$n=[x]$](images/img993.gif) をとる.
逆数をとって
をとる.
逆数をとって
これから
つまり
ところが
なので,はさみうちの原理から
である.
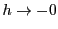 のときは.
のときは.
を示せばよい.同様にして
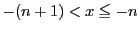 となる
となる をとると,
をとると,
これから
となり先の例題からこの場合も成立する.
□
これで自然体数の底といわれる定数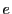 は定義された.
次に指数関数
は定義された.
次に指数関数
を定義しよう.指数関数は
 が自然数の範囲,正数の範囲,有理数の範囲と拡大されてきた.
底は実数値が一意に定まるために制限されてきた.
いま有理数の範囲では
が自然数の範囲,正数の範囲,有理数の範囲と拡大されてきた.
底は実数値が一意に定まるために制限されてきた.
いま有理数の範囲では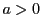 の定数に対して
の定数に対して
と定まっているものとする.
次のようにこれが実数に拡大できることを示す.
補題 3

を
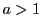
である定数とする.
自然数

をとり閉区間
![$I=[-N,\ N]$](images/img1006.gif)
において
とおく.このとき

は
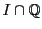
で一様連続である.
証明
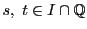 のとき
のとき
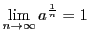 であるから,
正数
であるから,
正数 に対して
に対して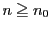 なら
なら
となる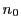 がある.このとき
がある.このとき
となり,一様連続である.
□
定義 19 (指数関数の定義)

は1でない正の定数とする.
有理数の

に対して関数値

は一意に定義されているものとする.
任意の実数

に対して

に収束する有理数列
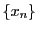
をとり.
で定義する.これによって実数を定義域とする一様連続関数が定義される.
■
証明
補題の設定を用いる.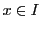 に対し
に対し に収束する
に収束する
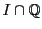 内の数列
内の数列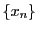 をとる.補題によって数列
をとる.補題によって数列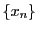 は
は 内の基本列であり,極限値をもつ.
よって
内の基本列であり,極限値をもつ.
よって は
は![$I=[-N,\ N]$](images/img1006.gif) の一様連続関数に拡張される.
の一様連続関数に拡張される. は任意であるから
は任意であるから は
は から
から
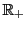 への一様連続関数に拡張された.
ただし
への一様連続関数に拡張された.
ただし
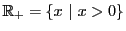 とする.
とする.
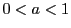 のときも同様である.
□
のときも同様である.
□
連続性から有理数における指数法則
は実数においても成立する.
指数関数 の逆関数を
の逆関数を
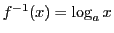 と表す.
と表す.
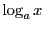 は
は
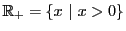 を定義域とし
を定義域とし を値域とする一様連続関数である.指数法則に対応して
を値域とする一様連続関数である.指数法則に対応して
が成り立つ.
実際,第1式は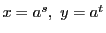 とおくと
とおくと
よりわかり,第2式は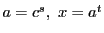 とおくと
とおくと
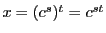 なので
なので
よりわかる.
以上によって,整式関数,有理関数,無理関数,三角関数と逆三角関数,指数関数と対数関数が定義された.これらを初等関数という.


 次: 微分の方法
上: 関数の概念
前: 一様連続
次: 微分の方法
上: 関数の概念
前: 一様連続
2014-05-23
![]() の集合である.
曲線の長さの定義にもとづいて円周もまた定義される.
半径1の時の円周の長さを
の集合である.
曲線の長さの定義にもとづいて円周もまた定義される.
半径1の時の円周の長さを![]() と定める.
と定める.
![]() となる円弧に対し,その中心角を
となる円弧に対し,その中心角を
![]() と定めるのである.弧度法による角は任意の実数値をとる.
と定めるのである.弧度法による角は任意の実数値をとる.
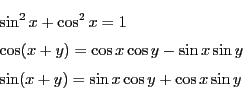
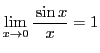 である.
■
である.
■
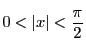 のとき,
のとき,
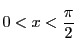 のとき.
点
のとき.
点 ![]() を中心とする半径1の円において,
中心角
を中心とする半径1の円において,
中心角 ![]() の扇形
の扇形 ![]() を考える.点
を考える.点![]() から
から
![]() に垂線
に垂線![]() を引く.
点
を引く.
点![]() において円に接線
において円に接線![]() を引く.
円弧の長さが内接多角形の長さの上限であり,
外接多角形の長さの下限であったので
を引く.
円弧の長さが内接多角形の長さの上限であり,
外接多角形の長さの下限であったので
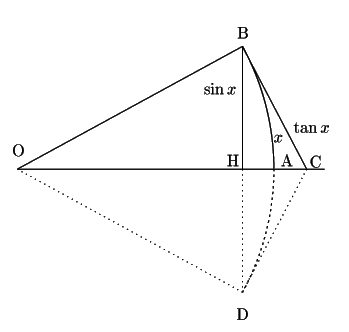
![]() が負のとき,
が負のとき, ![]() とおくと
とおくと
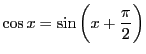 より
より
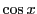 も一様連続である.
も一様連続である.
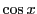 の連続性から
の連続性から


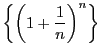 の収束や,
また
の収束や,
また
 が単調増加で有界であることを示せばよい.
が単調増加で有界であることを示せばよい.
![]() と表す.
と表す.
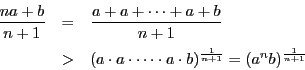
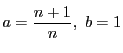 で用いると,
で用いると,
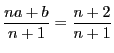 なので,
なので,
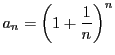 が単調増加であること示している.
が単調増加であること示している.
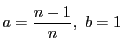 で用いると,
で用いると,
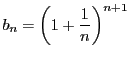 が単調減少であること示している.
また
が単調減少であること示している.
また
![]() の値もある程度計算できる.
の値もある程度計算できる.
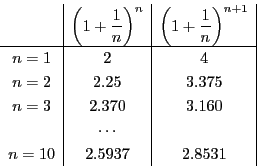
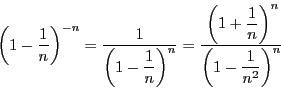
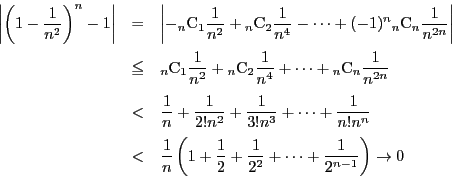
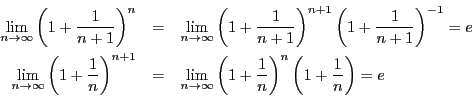
![]() のときは.
のときは.
![]() は定義された.
次に指数関数
は定義された.
次に指数関数
![]() のときも同様である.
□
のときも同様である.
□
![]() の逆関数を
の逆関数を
![]() と表す.
と表す.
![]() は
は
![]() を定義域とし
を定義域とし![]() を値域とする一様連続関数である.指数法則に対応して
を値域とする一様連続関数である.指数法則に対応して