が成立する.■
証明 任意の正数
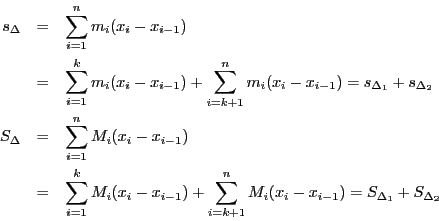
これを示す.![]() は連続なので原始関数が存在する.
それを
は連続なので原始関数が存在する.
それを![]() とおく.合成関数の微分法から
とおく.合成関数の微分法から
![\begin{eqnarray*}
\int_a^bf'(x)g(x)\,dx
&=&\int_a^b\dfrac{d}{dx}f(x)g(x)\,dx-\...
...g'(x)\,dx\\
&=&\Bigl[f(x)g(x)\Bigr]_a^b-\int_a^bf(x)g'(x)\,dx
\end{eqnarray*}](images/img1723.gif)

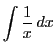 について.
について.
![]() は
は![]() で不連続である.
で不連続である.![]() の関数としては
の関数としては
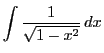 について.
について.
逆三角関数の定義の注意3.2,および初等関数の微分の逆三角関数の微分からわかるように,
![]() はともに
はともに
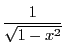 の原始関数である.
の原始関数である.
方法1
![]() とおく.ただし,
とおく.ただし,
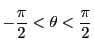 にとる.
にとる.
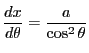 で,
で,
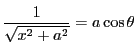 なので,
なので,
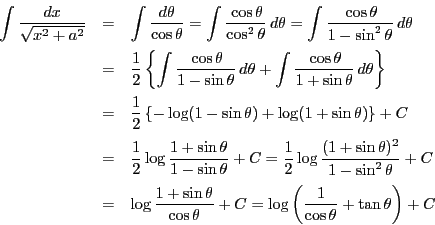
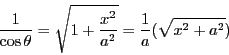
方法2
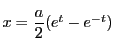 とおく.
とおく.
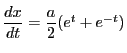 で,
で,
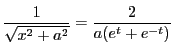 なので,
なので,
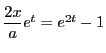 より
より
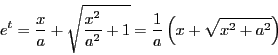
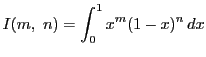 とおく.
とおく.
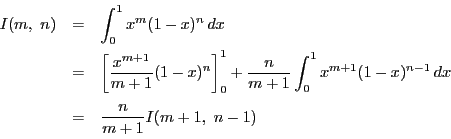
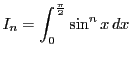 とおくと,
とおくと,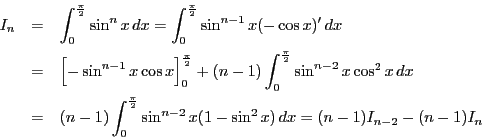
![\begin{displaymath}
\begin{array}{l}
\displaystyle I_0=\int_0^{\frac{\pi}{2}...
... x\,dx=\Bigl[-\cos x \Bigr]_0^{\frac{\pi}{2}}=1
\end{array}
\end{displaymath}](images/img1757.gif)
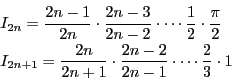
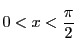 に対し
に対し
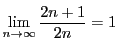 なので
なので
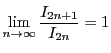 である.
である.
一般に
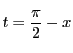 と置換することでわかる.
したがって
と置換することでわかる.
したがって
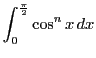 も同じ漸化式を満たす.
も同じ漸化式を満たす.