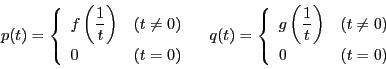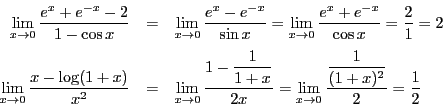次: 高次微分
上: 微分の方法
前: 微分計算
次: 高次微分
上: 微分の方法
前: 微分計算
微分の方法は関数の諸性質を解析するもっとも基礎となる方法である.そのためのいくつかの基本定理を証明する.
平均値の定理は微分法における最も重要な定理である.平均値の定理を証明するために, まずロルの定理を示す.
ロルの定理は,実数の完備性を根拠とする存在定理の典型である.
定理 37 (ロルの定理)
関数

は閉区間
![$[a,\ b]$](images/img797.gif)
で連続, 開区間

で微分可能であり,
かつ
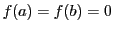
をみたすものとする. このとき
をみたす

が存在する.
■
証明
 が定数なら
が定数なら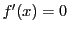 なので明らか.定数でないなら関数
なので明らか.定数でないなら関数 は閉区間で連続なので最大値と最小値が存在する.
は閉区間で連続なので最大値と最小値が存在する.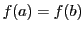 なので最大値か最小値のいずれかは
なので最大値か最小値のいずれかは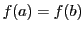 ではない.それを
ではない.それを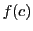 とする.
とする.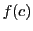 が最大値であるとする.
が最大値であるとする.
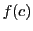 は最大値なので,
は最大値なので,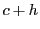 が区間に属するすべての
が区間に属するすべての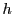 に対して
に対して
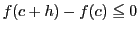 である.
である.
 は
は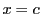 で微分可能なので,分母の符号を考え
で微分可能なので,分母の符号を考え
ゆえに
である.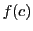 が最小値のときも同様である.
□
が最小値のときも同様である.
□
これを一般化することで平均値の定理が得られる.
定理 38 (平均値の定理)
関数

は閉区間
![$[a,\ b]$](images/img797.gif)
で連続, 開区間

で微分可能であるとする.
このとき
をみたす

が存在する.
■
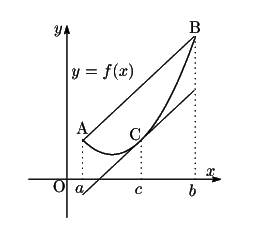 まず,平均値の定理はグラフでは何を意味するか. 関数
まず,平均値の定理はグラフでは何を意味するか. 関数 のグラフは,
ひとつながりになったなめらかな(連続かつ微分可能)曲線である.
その端点 A
のグラフは,
ひとつながりになったなめらかな(連続かつ微分可能)曲線である.
その端点 A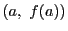 , B
, B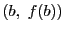 を結ぶ線分 AB の傾き
を結ぶ線分 AB の傾き
をとる.
この傾きと,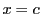 における接線の傾き
における接線の傾き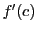 が等しくなる点 C
が等しくなる点 C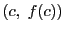 が曲線の端点 A と B の間に存在する.
が曲線の端点 A と B の間に存在する.
平均値の定理の証明
関数 に対し,定数
に対し,定数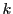 を
を
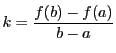 で定める.
で定める.
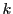 を用いて関数
を用いて関数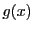 を
を
で定める.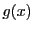 は閉区間
は閉区間![$[a,\ b]$](images/img797.gif) で連続, 開区間
で連続, 開区間 で微分可能であり,
で微分可能であり,
であるから,ロルの定理より
をみたす が存在する.
が存在する.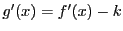 より
より
つまり題意をみたす が存在した.
□
が存在した.
□
系 38.1
開区間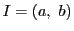 で微分可能な関数
で微分可能な関数 が
が で定数、単調増加、単調減少となる必要十分条件は
で定数、単調増加、単調減少となる必要十分条件は
証明
必要性は「関数の増減」で示されている.
逆に,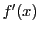 についてそれぞれの条件が成り立つとする.
このとき
についてそれぞれの条件が成り立つとする.
このとき
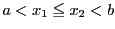 なる任意の
なる任意の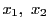 に対して
それぞれ
に対して
それぞれ
が成り立つ.したがって
が成り立つ.
□
系 38.2
開区間
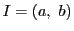
で微分可能な関数

が
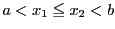
なる
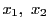
に対して
ならば
が成り立つ.
■
証明
同様に
が成り立つ.これから結論が得られる.
□
系 38.3

と
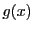
が閉区間
![$[a,\ b]$](images/img797.gif)
で連続, 開区間

で微分可能であるとする.このとき
ならば
が成り立つ.
■
証明
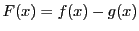 とし,
とし,
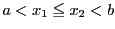 なる
なる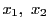 に対して
に対して
 で系38.2を用いると,
で系38.2を用いると,
関数の連続性から結論を得る.
□
系 38.4
関数

は
![$[a,\ b]$](images/img797.gif)
で連続,

で微分可能であるとする. このとき
となる
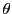
が少なくとも1つ存在する.
■
証明
平均値の定理38で 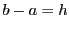 とおくと,
とおくと,
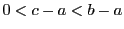 となるので
となるので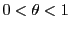 の範囲にある
の範囲にある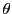 を用いて
を用いて
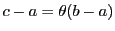 ,つまり
,つまり
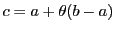 と書ける.
□
と書ける.
□

平均値の定理を二つの関数の商の形に一般化することができる.
定理 39
関数

,
は区間
![$[a,\ b]$](images/img797.gif)
で連続,

で微分可能で,かつこの区間でつねに
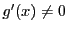
とする.
をみたす

が存在する.
■
証明
平均値の定理から
となる が存在する.そこで
が存在する.そこで
とおき,関数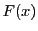 を
を
で定める.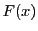 は区間
は区間![$[a,\ b]$](images/img797.gif) で連続,
で連続, で微分可能で,
で微分可能で,
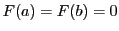 であるから,ロルの定理によって
であるから,ロルの定理によって
となる が
が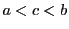 に存在する.
□
に存在する.
□
コーシーの平均値の定理も系38.4と同様に,
次の等式を満たす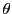 の存在とすることもできる.
の存在とすることもできる.
注意 4.2
コーシーの平均値の定理
39において
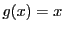
とすれば平均値の定理
38そのもになる.
この意味でコーシーの平均値の定理は平均値の定理の一般化である.
二つの関数 ,
,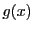 と定義域内の
と定義域内の がある.
がある.
商
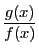 の
の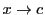 の極限は次のような場合は確定する.
の極限は次のような場合は確定する.
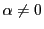 のとき.
のとき.
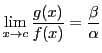
-
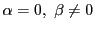 かつ
かつ の近くで
の近くで の符号が一定.
このときは,
の符号が一定.
このときは,
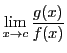 は
は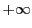 または
または
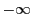 である.
である.
ところが
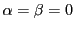 のときはさまざまの状況が起こり,
不定形といわれるものの一つである.
複雑な関数で不定形になる場合のうち,
コーシーの平均値の定理を応用して計算できる場合がある.
のときはさまざまの状況が起こり,
不定形といわれるものの一つである.
複雑な関数で不定形になる場合のうち,
コーシーの平均値の定理を応用して計算できる場合がある.
系 39.1 (ロピタルの定理)
二つの関数

,
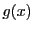
が

の近くで連続,

以外では微分可能とし,
とする.
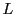
を有限確定値かまたは
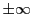
とする.
このとき
■
証明
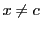 とする.
とする. と
と の間の
の間の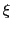 が存在して
が存在して
となるものがある.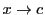 のとき
のとき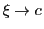 なので
右辺の極限値が
なので
右辺の極限値が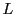 なら左辺の極限値も
なら左辺の極限値も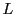 である.
□
である.
□
注意 4.3
この系の証明では,

と

の間での平均値の定理しか用いていないので,
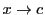
の代わりに
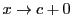
または
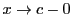
としても成り立つ.
系 39.2
二つの関数

,
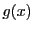
が区間
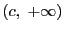
で微分可能で
とする.
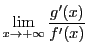
が存在するか,
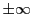
が確定すれば
■
証明
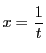 の置きかえをし
の置きかえをし
とする.これらは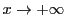 のとき
のとき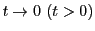 であり,
であり,
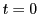 で連続,
で連続,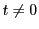 で微分可能である.
で微分可能である.
なので系39.1から
□
当然ロピタルの定理はくりかえして使うこともできる.
注意 4.4
このようにロピタルの定理は有用なものであるが次のような場合は
使ってはならない.
なぜかといえば,
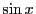
や
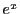
の微分にこれらの不定形の極限を使うから,
これでは循環論法になる.


 次: 高次微分
上: 微分の方法
前: 微分計算
次: 高次微分
上: 微分の方法
前: 微分計算
2014-05-23
![]() が定数なら
が定数なら![]() なので明らか.定数でないなら関数
なので明らか.定数でないなら関数![]() は閉区間で連続なので最大値と最小値が存在する.
は閉区間で連続なので最大値と最小値が存在する.![]() なので最大値か最小値のいずれかは
なので最大値か最小値のいずれかは![]() ではない.それを
ではない.それを![]() とする.
とする.![]() が最大値であるとする.
が最大値であるとする.
![]() は最大値なので,
は最大値なので,![]() が区間に属するすべての
が区間に属するすべての![]() に対して
に対して
![]() である.
である.
![]() は
は![]() で微分可能なので,分母の符号を考え
で微分可能なので,分母の符号を考え
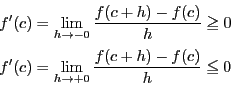
 まず,平均値の定理はグラフでは何を意味するか. 関数
まず,平均値の定理はグラフでは何を意味するか. 関数![]() に対し,定数
に対し,定数![]() を
を
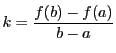 で定める.
で定める.
![]() を用いて関数
を用いて関数![]() を
を
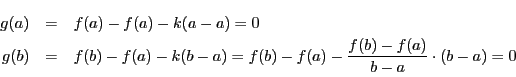
![]() で微分可能な関数
で微分可能な関数![]() が
が![]() で定数、単調増加、単調減少となる必要十分条件は
で定数、単調増加、単調減少となる必要十分条件は
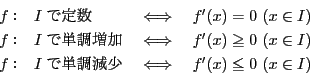

![]() の存在とすることもできる.
の存在とすることもできる.
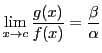
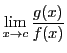 は
は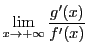 が存在するか,
が存在するか,