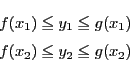次: 級数展開
上: 微分の方法
前: 関数解析
次: 級数展開
上: 微分の方法
前: 関数解析
関数 が与えられている.この関数を0回微分した関数は
が与えられている.この関数を0回微分した関数は 自身として,
自身として,
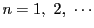 に対して
に対して 回微分を帰納的に次のように定義する.
回微分を帰納的に次のように定義する.
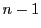 回微分した関数を
回微分した関数を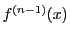 とする.
とする.
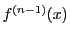 がふたたび微分可能なとき
がふたたび微分可能なとき
 は
は 回微分可能であるといい,
回微分可能であるといい,
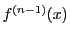 の導関数
の導関数
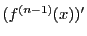 を
を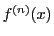 と書く.
これを
と書く.
これを の第
の第 次導関数という.
これによって,帰納的に第
次導関数という.
これによって,帰納的に第 次導関数が定義される.
次導関数が定義される.
定理 40
関数

と
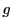
は

回微分可能であるとする.
定数

,
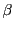
に対して
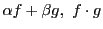
はそれぞれ

回微分可能で
- (1)
-
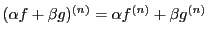
- (2)
-
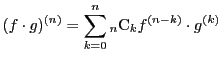
となる.
■
証明
数学的帰納法で示す.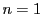 のときは定理35より成立.
のときは定理35より成立.
 のときに成立するとする.
のときに成立するとする.
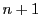 のとき.
のとき.
となり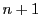 のときも成立する.
よってすべての自然数に対して定理が成立する.
□
のときも成立する.
よってすべての自然数に対して定理が成立する.
□
つぎの定理は定理35の(3),および定理36の(4)(5)
を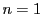 のときとし,後はこれらをくりかえし用いることで数学的帰納法によって成立する.ただ一般形を書くことは,
のときとし,後はこれらをくりかえし用いることで数学的帰納法によって成立する.ただ一般形を書くことは,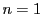 の場合のように簡単ではない.
の場合のように簡単ではない.
開区間 で微分可能な関数
で微分可能な関数 の導関数
の導関数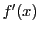 がふたたび微分可能であるとき
がふたたび微分可能であるとき
 は二回微分可能であるという.
は二回微分可能であるという.
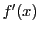 の導関数を第二次導関数といい
の導関数を第二次導関数といい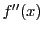 と書く.
第二次導関数については次のような記号も用いる.
と書く.
第二次導関数については次のような記号も用いる.
第二次導関数の計算公式などは次の第 次導関数のところで統一して示す.
ここでは,第二次導関数の幾何的意味について考える.
第二次導関数の符号が一定なら,
接線の傾きが単調に変化することを意味し,
グラフの形状が,いわゆる「上に凸」や「下に凸」
といわれるものになる.
これらの概念をもう少し正確に考えていこう.
そのためにいくつかの定義を導入し,いくつかの定理を証明する.
次導関数のところで統一して示す.
ここでは,第二次導関数の幾何的意味について考える.
第二次導関数の符号が一定なら,
接線の傾きが単調に変化することを意味し,
グラフの形状が,いわゆる「上に凸」や「下に凸」
といわれるものになる.
これらの概念をもう少し正確に考えていこう.
そのためにいくつかの定義を導入し,いくつかの定理を証明する.
 定義 23
定義 23
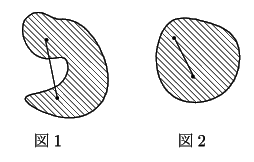
平面の領域

内の任意の2点
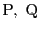
に対し
線分
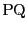
が

に含まれるとき,
領域

は
凸領域であるという.
■
定理 42
関数

は

で定義され,この区間で二回微分可能であり,
かつこの区間で
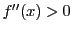
とする.
定義域内の任意の二つの

の値
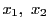
と
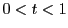
なる実数
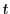
に対して
が成立する.
■
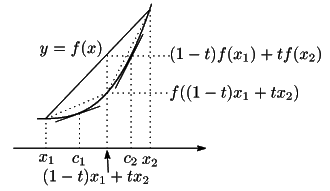
証明
 のときは等号が成立する.
のときは等号が成立する.
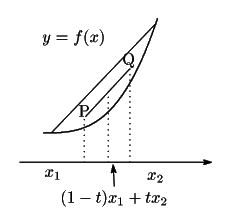
いま とする.すると
とする.すると
である.区間
![$[x_1,\ (1-t)x_1+tx_2]$](images/img1283.gif) と
と
![$[(1-t)x_1+tx_2,\ x_2]$](images/img1284.gif) に平均値の定理を用いる.それぞれに対応する開区間内の
に平均値の定理を用いる.それぞれに対応する開区間内の を用いて
を用いて
となるものが存在する.
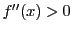 より
より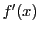 が単調増加なので
が単調増加なので
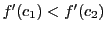 ,つまり
,つまり
これを整理して
を得る. で等号のときとあわせて本定理が示された.
□
で等号のときとあわせて本定理が示された.
□
これは次のように一般化される.
系 42.1
関数

は区間
![$I=[a,\ b]$](images/img1290.gif)
で定義され,この区間で二回微分可能であり,
かつこの区間で
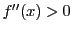
とする.

を二以上の自然数とする.
定義域内の任意の

個の

の値
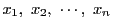
と
正で
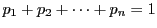
なる実数
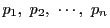
に対して
が成立する.
■
証明
数学的帰納法で示す.
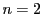 のときは定理42から成立.
のときは定理42から成立.
 個の場合に成立するとし
個の場合に成立するとし 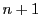 個の場合に成立することを示す.
個の場合に成立することを示す.
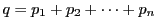 とおく.
とおく.
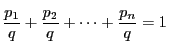 および
および
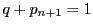 であることに注意する.
であることに注意する.
ゆえに 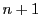 の場合も成立した.
等号成立は
の場合も成立した.
等号成立は
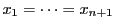 のとき.
よって一般の
のとき.
よって一般の  に対して題意が示された.
□
に対して題意が示された.
□
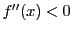 のときは不等号の向きが逆になる.その他は同じである.
この不等式は多くの絶対不等式を作り出す.
のときは不等号の向きが逆になる.その他は同じである.
この不等式は多くの絶対不等式を作り出す.
例 4.3
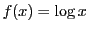
とすると,定義域は
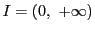
で
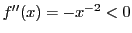
である.
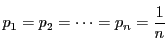
で用いると
である.これから相乗平均・相加平均の不等式が得られる.
定義 24
閉区間
![$I=[a,\ b]$](images/img1290.gif)
で定義された関数

がある.
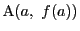
,
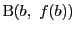
とする.
平面におけるグラフの曲線
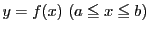
と
線分
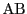
で囲まれた領域

が凸であるとき,
関数

を凸関数という.
 が区間
が区間
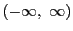 や
や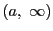 ,
また
,
また などの,端点が
などの,端点が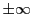 である場合を含む開区間で
定義されているときは,その区間内の任意の閉区間で凸関数であるとき,
である場合を含む開区間で
定義されているときは,その区間内の任意の閉区間で凸関数であるとき,
 を凸関数であるという.
■
を凸関数であるという.
■
 はつぎのように記述される.
はつぎのように記述される.
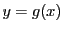 を直線
を直線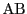 の方程式とする.
の方程式とする.
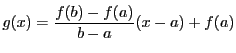 である.
である.
系 42.2
関数

は区間
![$I=[a,\ b]$](images/img1290.gif)
で定義され,この区間で二回微分可能であり,
かつこの区間で
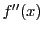
の符号が一定である.このとき

は凸関数である.
■
証明
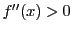 とする.
とする.
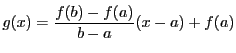 とするとき
とするとき において
において
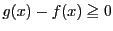 が成り立つことを示す.
が成り立つことを示す.
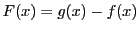 とおく.
とおく.
である.
平均値の定理から
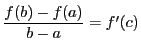 となる
となる が区間
が区間 に存在する.
に存在する.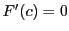 かつ
かつ
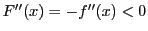 より
より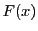 は
は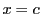 で極大で最大である.
で極大で最大である.
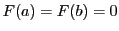 となるので,
となるので, で
で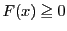 であることが示された.
よって領域
であることが示された.
よって領域
が凸であることを示せばよい. の2点
の2点
 をとり
をとり
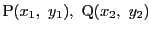 とする.また線分
とする.また線分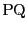 上の点
上の点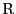 を
を
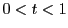 の範囲の実数
の範囲の実数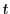 を用いて
を用いて
 とおく.
とおく.
 が
が の点なので
の点なので
が成り立つ.それぞれ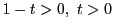 を乗じて加えることにより
を乗じて加えることにより
が成り立つ.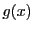 は
は
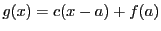 と1次関数なので,
と1次関数なので,
である.
定理42から
なので
が成立する.
つまり点
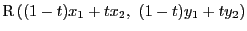 も領域
も領域 に属することが示された.よって
に属することが示された.よって は凸領域であり,
は凸領域であり,
 は凸関数である.
は凸関数である.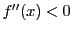 のときもまったく同様に示される.
□
のときもまったく同様に示される.
□


 次: 級数展開
上: 微分の方法
前: 関数解析
次: 級数展開
上: 微分の方法
前: 関数解析
2014-05-23
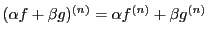
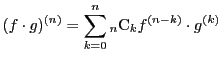
![]() のときに成立するとする.
のときに成立するとする.
![]() のとき.
のとき.
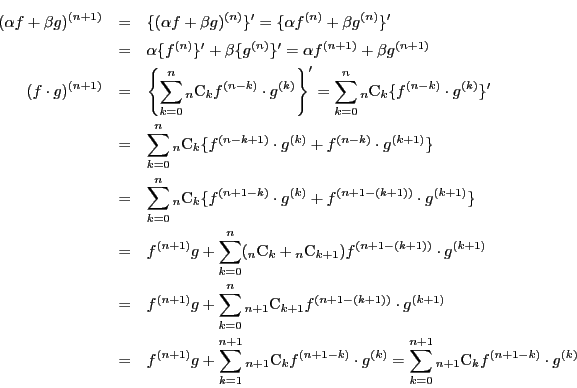
![]() のときとし,後はこれらをくりかえし用いることで数学的帰納法によって成立する.ただ一般形を書くことは,
のときとし,後はこれらをくりかえし用いることで数学的帰納法によって成立する.ただ一般形を書くことは,![]() の場合のように簡単ではない.
の場合のように簡単ではない.
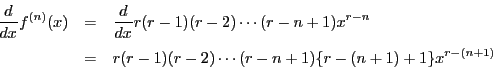
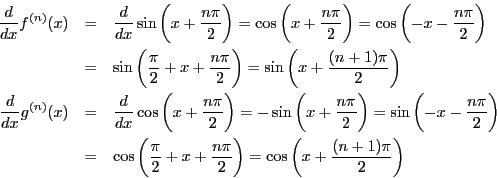
 定義 23
平面の領域
定義 23
平面の領域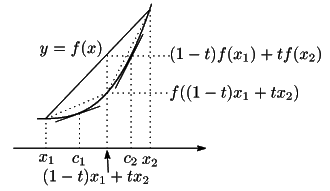
![]() とする.すると
とする.すると
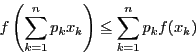
![]() 個の場合に成立するとし
個の場合に成立するとし ![]() 個の場合に成立することを示す.
個の場合に成立することを示す.
![]() とおく.
とおく.
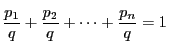 および
および
![]() であることに注意する.
であることに注意する.
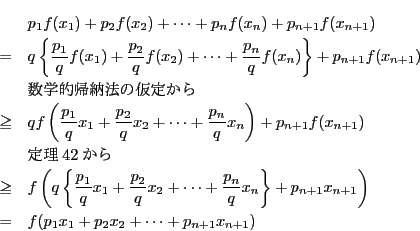
![]() のときは不等号の向きが逆になる.その他は同じである.
この不等式は多くの絶対不等式を作り出す.
のときは不等号の向きが逆になる.その他は同じである.
この不等式は多くの絶対不等式を作り出す.
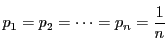 で用いると
で用いると
![]() が区間
が区間
![]() や
や![]() ,
また
,
また![]() などの,端点が
などの,端点が![]() である場合を含む開区間で
定義されているときは,その区間内の任意の閉区間で凸関数であるとき,
である場合を含む開区間で
定義されているときは,その区間内の任意の閉区間で凸関数であるとき,
![]() を凸関数であるという.
■
を凸関数であるという.
■
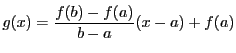 である.
である.
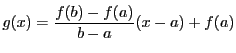 とするとき
とするとき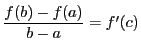 となる
となる とおく.
とおく.