高校の解析学

教科書の変化

解析学の方法は単純明快なもので力強い．すべてを実数論に根拠づけることができる．ところが，日本の高校解析の教科書は年々内容が薄くなり，理論構成が煩雑で力強さを失っている．論述も感覚的な解説に頼って命題が成立する根拠を問うことがたいへん弱い．そのため立ちかえるべき地点が見えず，よけいに理解が困難になっている．

1960年代以降の日本の高校数学における微分・積分の取り扱い方の変遷を確認しよう．資料として次のものを用いた．

$\maru{1}\$ 1965年教科書（数研出版）のI，IIB． $\maru{2}\$ 1969年教科書（日本書院）のI，IIB，III． $\maru{3}\$ 1982年問題新集（科学新興社）のI，代数・幾何，基礎解析，微分・積分． $\maru{4}\$ 1997年教科書（数研出版）のI，A，II，B，III，C． $\maru{5}\$ 2005年教科書（数研出版）の一部写し． $\maru{5}\$ 2014年教科書（数研出版）I，A，II，B，III．

これを見るとそれぞれにつぎのような特徴がある．

1) 1965年，1969年のものでは，数列の極限と無限級数まで数学IIBの範囲，つまり文理共通範囲であった．極限が数学IIBの微分法で必要な以上，数列およびその和の極限移行まで数学IIBに置くのは自然である．

面積の定義が，小正方形による内からの近似，およびその極限としてなされる．その上で区分求積による面積計算がなされ，それを踏まえて区間を等分したリーマン和によって定積分が定義される．その定義にもとづいて，定積分が原始関数の値の差と一致することが証明される．

数学IIIにおいて，平均値の定理について．1969年には「微分法」のなかで連続関数の最大最小値の存在を根拠に微分の定義から証明されている．

また，定積分の定義では，任意の小区間についてのリーマン和で定義される．そして定積分の平均値の定理から，連続関数に対して，積分法は微分法の逆演算であることを示している．

2) 80年代に用いられた基礎解析と微分・積分では，数列の極限と無限級数が微分・積分に移行する．平均値の定理と定積分の定義は，60年代の方法をそのまま継承している．

3) 1997年の教科書はこれらと大きく変わる．平均値の定理が「微分法の応用」の「発展」として扱われ，必須でなくなる．

数学IIで面積が無定義に用いられ，関数のグラフと軸で囲まれる領域の面積を，方向で微分するともとの関数になることが示される．面積の微分がとなることを数学IIで示す．そしてこれを原始関数が存在する根拠に用いて，定積分を原始関数の値の差で定義した．つまり，積分を，微分を前提として定義した．

この定積分の定義は，数学IIIでも変わらない．

4) 2005年には平均値の定理が証明なしに「知られている」として扱われるようになり，平均値の定理の根拠が示されなくなった．

定積分の定義は，90年代のものがそのまま移行する．

5) 2014年版では，平均値の定理が，「発展」として，閉区間での連続関数が最大値，最小値をもつことを根拠に，ロルの定理を経て証明がなされる．さらにこの根拠は「実数の本質に基づくものであり」云々の記述があり，90年代～00年代の従来のものより改善されたといえる．これがこの教科書だけのことであるのかどうかは，点検しえていない．

一方，2014年版では，次のような記述が現れる．

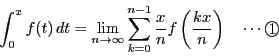
$\begin{displaymath} \int_0^xf(t)\,dt=\lim_{n \to \infty}\sum_{k=0}^{n-1}\dfrac{x}{n}f\left(\dfrac{kx}{n} \right)\quad \cdots\maru{1} \end{displaymath}$

歴史的には，定積分は①で定義された．

教科書の著者は，この記述で，本来はこれが定積分の定義であるということが言いたかったのかも知れない．しかし，この教科書の文面からは，かつてはこのように定義されていたが今は違う，と誤ったことが高校生に伝わる．あるいは，原始関数の値の差として定義する現行の定義の方が正しい定義であると高校生が誤解する．

また，2014年版では，面積をリーマン和で表すことは発展的解説の中で復活する．ところが

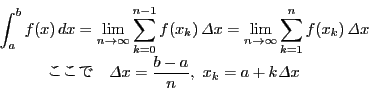
$\begin{displaymath} \begin{array}{l} \displaystyle \int_a^bf(x)\,dx =\lim_{n ... ...lta} x=\dfrac{b-a}{n},\ x_k=a+k\mathit{\Delta} x \end{array} \end{displaymath}$

定積分を，上のような和の極限として求めることを，定積分の区分求積法という。

との記述がなされる．

まず，「求積」とは『解析概論』の第3章冒頭「28　古代の求積法」にあるように，一貫して面積や体積を求めることであった．ところがここでは定積分を求めることとされている．また，「定積分を和の極限として求める」と書かれているが，現行高校数学の体系をおいて，本来の解析学の立場でいえば，これは右辺の和の極限が左辺の定積分の定義なのであって，一方から他方を求めるということではない．

さらに，実際に高校生がやることは，そしてまたこの教科書の例題にもあることは「数列の和の極限を定積分で計算する」ことである．この記述と実際は逆である．これをまじめに読んだ高校生は，習ったことと逆で，いったい何が言いたいのかまったく理解できないだろう．

以上、各時代の教科書の特徴点をあげた．1997年以降，リーマン和を定積分の定義とすることを避けている．ここに現行の日本の高校教科書の特質がある．その結果，さまざまの矛盾や堂々巡りを繰り返す解説となる．定積分を原始関数の値の差で定義することに無理がある．このような定義を教科書に載せているのは日本くらいなものである．この誤りを正すことなく教科書をつくるので，いろんなところで矛盾が出るし，記述が混乱する．

実際に多くの制約の中で教科書をつくる困難は理解する．しかし，これは制作者の良心の問題である．教科書の変化は日本の科学教育の混乱と衰退を象徴している．この40年間，日本の高校での微分法・積分法は衰退し続けてきた．このようなことでは，ますます科学離れが進み，若者の考える力が衰えていく．

せめて1960～80年代の教科書の立場に立ち返ることができなければならない．あるいは，文明の現段階に応じて，過去の遺産を継承し，その上で新たな表現とそれを伝える方法を見出さなければならない．そのためにも，高校生に伝えるべき内容とその背景に関する過去の遺産をまとめることは，必要な一里塚である．

2014-05-23