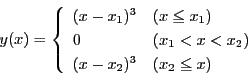 平面で定義された関数
平面で定義された関数
このように
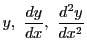 等の未知関数とその導関数が,他の定まった関数と結びついて作られる
等の未知関数とその導関数が,他の定まった関数と結びついて作られる
未知な関数とその導関数,および定関数を含む等式として,
微分方程式は大変広い一般的な概念であり,また発展する概念である.未知関数も複数個あり,それらのなすベクトル値関数が未知関数となってもよい.含まれる導関数の最も高い次数が![]() であるとき,これを
であるとき,これを![]() 階微分方程式という.ベクトル値関数の各成分を構成する未知関数が一変数の微分方程式を常微分方程式,多変数の微分方程式を偏微分方程式ということが多い.
さらに,
階微分方程式という.ベクトル値関数の各成分を構成する未知関数が一変数の微分方程式を常微分方程式,多変数の微分方程式を偏微分方程式ということが多い.
さらに,
与えられた微分方程式を満たす関数を微分方程式の解といい,解を求めることを微分方程式を解くという.
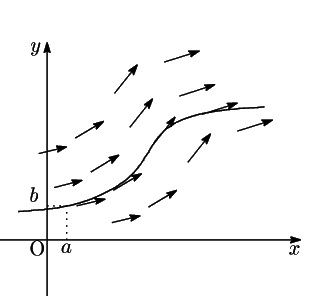
後に示すように微分方程式
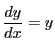 は解
は解![]() をもつ.実際これが微分方程式を満たすことは確認できる.微分方程式を解いて表れる定数
をもつ.実際これが微分方程式を満たすことは確認できる.微分方程式を解いて表れる定数![]() のことを任意定数という.
任意定数を含んだ解を一般解,任意定数に特別の値を与えて得られる解を特殊解という.
のことを任意定数という.
任意定数を含んだ解を一般解,任意定数に特別の値を与えて得られる解を特殊解という.![]() のとき
のとき![]() のような条件をつければ
のような条件をつければ![]() と一意に定まる.いくつかの変数値に対する与えられた関数値を微分方程式の初期条件という.
と一意に定まる.いくつかの変数値に対する与えられた関数値を微分方程式の初期条件という.
微分方程式は,実在する世界の現象を数学的にとらえるためのもっとも基本的な方法である. 数学の側では,ある種の基本的な微分方程式について, その解の存在定理を実数の完備性にもとづいて証明しなければならない.
本節冒頭の微分方程式
解が常に存在する,あるいは一意に存在するということは,一般的には成り立たない.
初期条件を満たすものが一意に存在する十分条件として
![]() につてのリプシツの条件がある.
につてのリプシツの条件がある.
![]() が
が![]() において偏導関数
において偏導関数
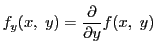 をもち,
をもち,
![]() が有界連続なら,平均値の定理から
が有界連続なら,平均値の定理から![]() はリプシツの条件を満たす.
はリプシツの条件を満たす.
証明
正数![]() と
と![]() に対し,
点
に対し,
点
![]() を中心とする二辺の長さが
を中心とする二辺の長さが![]() の長方形
の長方形![]() をとる.
をとる.
閉区間![]() 上の連続関数空間
上の連続関数空間![]() に
距離
に
距離![]() を
を
![]() から
から![]() への写像
への写像![]() を次のように定める.
を次のように定める.
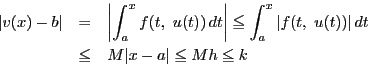
![]() は縮小写像である.なぜなら,
は縮小写像である.なぜなら,
![]() とし
とし
![]() とすると
とすると
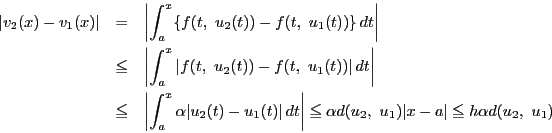
定理72によって![]() はただ一つの不動点
はただ一つの不動点
![]() をもつ.
をもつ.
証明の勘所は微分方程式6と初期条件を,
一つの積分方程式7になおす.
![]() が関数空間の縮小写像であることから,
が関数空間の縮小写像であることから,![]() となる
となる![]() の存在を示す.
このような道筋をたどるのであった.
の存在を示す.
このような道筋をたどるのであった.
定理72の証明で構成した数列は,この解の構成方法でもある. それを次の例で見てみよう.
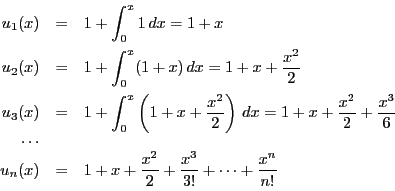
逆にリプシツ条件を満たさないときは, 存在しない場合や一意でない場合が現れる. よく知られた一意性の崩れる場合を例示しよう.
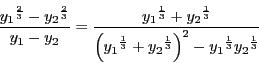
![]() とすると
とすると