001a

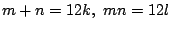2. $m+n=12k,\ mn=12l$ なら， mn=m(12k-m)=12l ．つまり m²=12(mk-l) ． m² が12の倍数なので， m は素因数2と3を持つ．つまり6の倍数．このとき n=12-m から n も6の倍数．
逆に 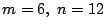$m=6,\ n=12$ とすると m+n=18 は12で割り切れない．よって，(c)．
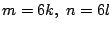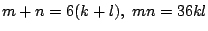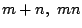$m=6k,\ n=6l$ とかける．さらに $m+n=6(k+l),\ mn=36kl$ なので， $m+n,\ mn$ が12の倍数になるためには k と l の偶数と奇数が一致すればよい．
　 k=1 に対して 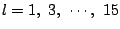$l=1,\ 3,\ \cdots ,\ 15$ の8個．
　 k=2 に対して 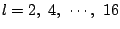$l=2,\ 4,\ \cdots ,\ 16$ の8個．
　 k=3 に対して 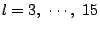$l=3,\ \cdots ,\ 15$ の7個．
　 k=4 に対して 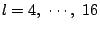$l=4,\ \cdots ,\ 16$ の7個．
　 $\cdots$
　 k=15 に対して 15 の1個．
　 k=16 に対して 16 の1個．

$\begin{displaymath}∴ \quad 2(8+7+\cdots+1)=72（個） \end{displaymath}$

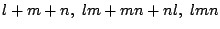3. $l+m+n,\ lm+mn+nl,\ lmn$ がすべて5で割り切れるとする． lmn が5の倍数なので少なくともひとつ，例えば l は5の倍数．するとその結果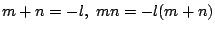， $m+n=-l,\ mn=-l(m+n)$ が5の倍数．
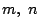$m,\ n$ の少なくとも一つは5の倍数． m が5の倍数なら n=-m も 5の倍数．条件は 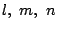$l,\ m,\ n$ で対称なので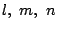， $l,\ m,\ n$ は5の倍数．
逆は明らか．よって，(a).

4. (3)より 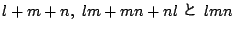$l+m+n,\ lm+mn+nl\ と\ lmn$ が5で割れることは同値である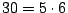． $30=5 \cdot 6$ で5と6は互いに素なので，6で割り切れることについて調べる．
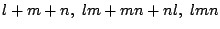$l+m+n,\ lm+mn+nl,\ lmn$ がすべて6で割り切れるとする．
　lmn が6の倍数なので，例えば l は2の倍数である．このとき(3)と同様にして 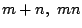$m+n,\ mn$ ともに2の倍数．よって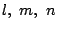， $l,\ m,\ n$ はすべて2の倍数．
　同様に l が3の倍数とすると 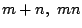$m+n,\ mn$ ともに3の倍数．よって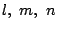， $l,\ m,\ n$ はすべて3の倍数．
よって 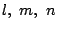$l,\ m,\ n$ は6の倍数．よって 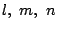$l,\ m,\ n$ は30の倍数．逆は明らか．∴　(a)．
30の倍数の組は

$\begin{eqnarray*}(l,\ m,\ n)&=&(30,\ 30,\ 30),\ (30,\ 30,\ 60),\ (30,\ 30,\ 90),... ...60,\ 60),\ (60,\ 60,\ 90),\ (60,\ 90,\ 90)\\ &&(90,\ 90,\ 90) \end{eqnarray*}$