行列
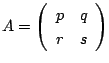 に対して,
に対して,
![]() とおく.このとき,次の問いに答えよ.ただし, E は2次の単位行列であり, A=kE となる実数 k は存在しないものとする.
とおく.このとき,次の問いに答えよ.ただし, E は2次の単位行列であり, A=kE となる実数 k は存在しないものとする.
- 1.
A2=tA-dE となることを示せ.
- 2.
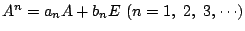 とするとき,
とするとき,
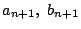 を
を
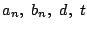 を用いて表せ.
を用いて表せ.
- 3.
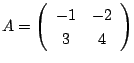 のとき,
のとき,
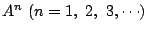 を求めよ.
を求めよ.
- 2.
静岡大問題 解答 解説 2000年入試に戻る
行列
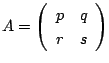 に対して,
に対して,
![]() とおく.このとき,次の問いに答えよ.ただし, E は2次の単位行列であり, A=kE となる実数 k は存在しないものとする.
とおく.このとき,次の問いに答えよ.ただし, E は2次の単位行列であり, A=kE となる実数 k は存在しないものとする.
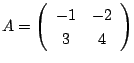 のとき,
のとき,