No Title

東大理 I 後期総合科目II １　解答　解説　 2001年入試に戻る

　昆虫の増殖や人口問題を扱う，数理生態学という学問分野がある．ベルハルスト(1845) は，生物の増殖に関する有名な方程式を提案している．その内容の概略は以下の通りである．
　ある生物の個体数を x，単位時間あたりの増加数を y とする． $x,\ y$ の間には， $y=\gamma x$ なる関係がある．ここで， $\gamma$ を増殖率と呼ぶ．ある生態系における生物の増殖を長時間観察すると増殖率 $\gamma$ は一定ではなく，個体数の変化に伴って 1次関数的に変化することが分かっており，これを考慮すれば， $\gamma=a(1-bx)$ と表せる．これより，個体数の時間的な変化を表す次の式が得られる．

$\begin{displaymath}\dfrac{dx}{dt}=a(1-bx)x \end{displaymath}$

(1)

　ただし， $a,\ b$ は正の定数である．これをロジスティック方程式と呼ぶ．

　式(1)を解いて， x を時刻 t=0における初期値 $x_0\ (x_0>0)$ と時間 t の関数として表す手続きに関する以下の設問に答えよ．

1 $s=\dfrac{1}{x}$ と変数変換し，式(1)から $\dfrac{ds}{dt}$ を s の関数として表せ．

2 1　で得られた式を解いて， s を求めよ．

3 初期条件を適用して， x を初期値 x₀ と時間 t の関数として表せ．

　式(1)の左辺の微分を，次の式で近似する．ただし， ${\it\Delta}t$ は正とする．

$\begin{displaymath}\dfrac{dx}{dt}=\dfrac{x(t+{\it\Delta}t)-x(t)}{{\it\Delta}t} \end{displaymath}$

(2)

　式(2)を式(1)の左辺に代入すると $x(t+{\it\Delta}t)-x(t)$ と x(t) の関係式が得られる．なお，式(1)の右辺の x には， x(t) を代入するものとする．
　さて，この生物は一定の時間間隔で一斉に生殖し，世代交代するものと仮定する．ここで，連続的な時間 t について考察する代わりに，自然数で表される「世代」を考える．
　式(2)の分母の ${\it\Delta}t$ を１つの世代の時間間隔，また，分子の $x(t+{\it\Delta}t)-x(t)$ を第 n+1 世代の個体数 x_n+1 と第 n 世代の個体数 x_n の差と見なし，

$\begin{displaymath}A=1+a{\it\Delta}t，u_n=\dfrac{ab{\it\Delta}t}{A}x_n \end{displaymath}$

(3)

と置けば，ロジスティック写像と呼ばれる次の方程式が得られる．

u_n+1=f(u_n)=A(1-u_n)u_n

(4)

　ここで， f(u_n) は u_n から u_n+1 を求める関数であり，これを写像 f と呼ぶ．
　いま，u_n の定義域を閉区間 $0\le u_n \le 1$ とし， $1<A\le 4$ であるとする．このとき u_n から u_n+1 ヘの写像fによって得られるu_n+1の値域は閉区間 $0\le u_n \le 1$ に入る．この写像からu_n+1の様々な挙動が発生する．以下では，図式を用いて A の値を小さい方から大きい方ヘと変化させた時のu_n+1の挙動を求めることにする．
　図式解法の手順を示す．図1の放物線は，式(4)を u_n を横軸，u_n+1を縦軸として表したものである．ただし，A=3.2である．第 0 世代に対応する初期値を u₀ とし，この値を出発点とし，写像 f を n 回繰り返すことで u_n が求められる．
　縦軸上で得られた値を横軸に折り返し，写像 f を逐次繰り返すと図 2(分かりやすくするために隣り合う点を直線で結んである)のような u_n の時間的変化が求められる．この操作によって求められる $u_0,\ u_1,\ u_2,\ \cdots$ を時系列と呼ぶ．この操作の手順は，写像 f を表す放物線と縦軸の値を横軸の値に写す写像を表す u_n+1=u_nを用いて，図式的に示すことができる．まず，横軸上の初期値 u₀から出発して，縦方向に移動して放物線と交わる点 u₁を求める．その後，横方向に移動して直線と交わる点を求める．この点を出発点として，同じ操作を行うことにより u₂が求まる．この操作を繰り返すことにより，時系列が求められる．

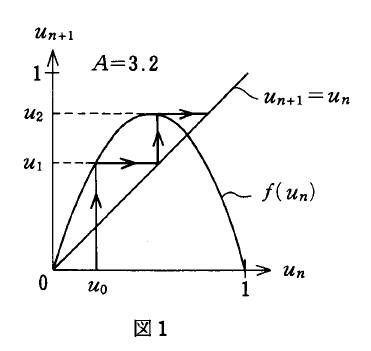
4 A=1.5の場合について，初期値 u₀ を0.25にとって上記の操作を行い， $u_1,\ u_2$ を求めよ．

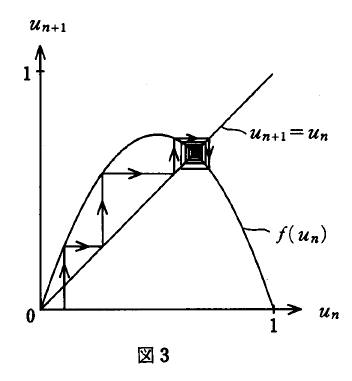
5 A が大きい場合には，写像fを繰り返すと， u_n は図3に示すように特定の値に収束する．これを1回写像の固定点と呼ぶ．この点に対応する u_n を A の関数で表せ．

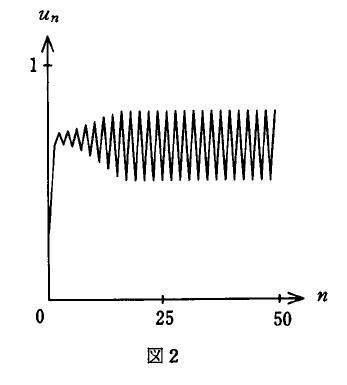
6 さらに A が大きい場合には，図2の例のように u_n は時間が経過するとともに振動的挙動を示す．このときの挙動を検討するために，写像 f を2回繰り返す f² について考察する．ここで， f² は u_n から u_n+2への写像であり， $u_{n+2}=f^2(u_n)=f\{f(u_n)\}$ と表せる． f² を A と u_n で表せ．

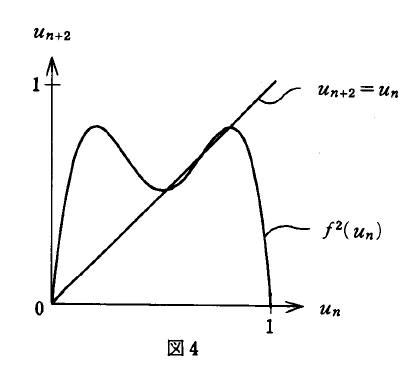
7 u_n+2=f²(u_n) を図示したものが図4である．この関数は， u_n+2=u_nの直線と4回交わる．この4つの交点のうち 1つは，1回写像の固定点である．このことを使って，残る3点に対応する u_n を求めよ．

　図2のようなケースを2周期的変化(注 : 1回おきに同じ値をとるような変化のこと)と呼ぶ．さらに大きな A についてこのような検討を行えば，4周期的変化，8周期的変化，…が得られ， $A>3.5699456\cdots$ では，非周期的変化に変わる.
　非周期的変化を示すA=4 の場合

$\begin{displaymath}u_n=\sin^2(\pi \theta_n) \quad (ただし\ 0 \le \theta_n \le 1 \ である) \end{displaymath}$

(5)

と置いて式(4)に代入すれば，u_n+1と u_n との関係は， $\theta_{n+1}$ と $\theta_n$ の関係に帰着できる．

8 $\theta_{n+1}$ と $\theta_n$ との間の関係式を求めよ．さらに，横軸に $\theta_n$ ，縦軸に $\theta_{n+1}$ をとり， $\theta_n$ から $\theta_{n+1}$ ヘの写像を図示せよ．