次: 3.
上: 2. 解答
前: 1.
x と y の連立方程式
が異なる四つの実数解(の組)を持てばよい.
 から
y2=4(1-x2).一つの x の値に対して実数 y が二つ定まるのは,
から
y2=4(1-x2).一つの x の値に対して実数 y が二つ定まるのは,
-1<x<1
のときである.
 から y を消去して整理した
から y を消去して整理した
が x の二次方程式なので,求める条件は 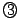 が -1<x<1に異なる二つの実数解を持つ
ことと同値である.
が -1<x<1に異なる二つの実数解を持つ
ことと同値である.
f(x)=3x2+2ax-a2+b-4 とおき,
D/4=a2-3(-a2+b-4) とする.放物線 y=f(x) の軸は
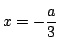 であるから,条件は
であるから,条件は
これを整理して,
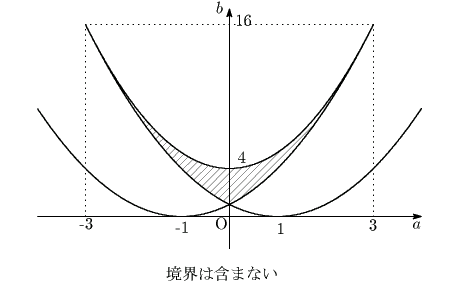
図は次のようになる.
AozoraGakuen
2002-03-16
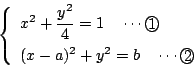
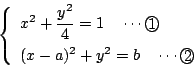
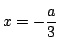 であるから,条件は
であるから,条件は