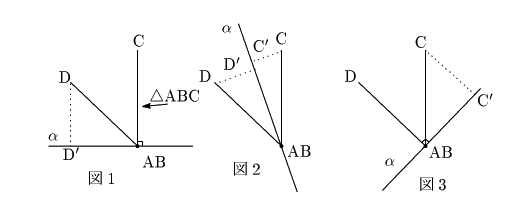
 3つの図は線分
AB の方から見たものである.
3つの図は線分
AB の方から見たものである.
はじめ ![]() を図1のように
を図1のように
![]() と垂直であるようにおく.
このとき
と垂直であるようにおく.
このとき
![]() が鋭角三角形なので,
点
C' は線分
AB 上にある.
が鋭角三角形なので,
点
C' は線分
AB 上にある.
したがって連続関数の中間値の定理によって, ![]() が図の範囲を動くとき
途中で
が図の範囲を動くとき
途中で
※別解
![]() を動かす範囲をもう少し狹めてもできる.
を動かす範囲をもう少し狹めてもできる.
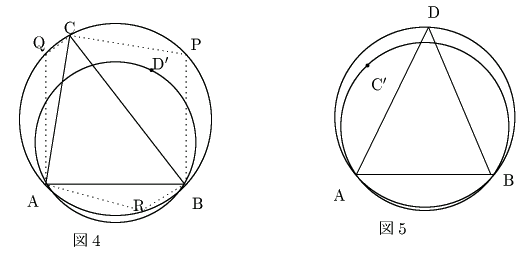
![]() を
を
![]() が
が ![]() 上にあるところから
上にあるところから
![]() が
が ![]() 上にあるようになるまで,上と同じく
上にあるようになるまで,上と同じく
![]() が線分
ABに
関して同じ側にあるように連続的に動かす.
が線分
ABに
関して同じ側にあるように連続的に動かす.
![]() が
が ![]() 上にあるとき,
D' はどこにあるか.
上にあるとき,
D' はどこにあるか.
ここで,
![]() の外接円をかき,
の外接円をかき,
![]() の各頂点から各辺に垂直な直線を引くと,
それらは2本ずつ外接円周上で交わる.例えば
AR と
BRについて,
の各頂点から各辺に垂直な直線を引くと,
それらは2本ずつ外接円周上で交わる.例えば
AR と
BRについて,
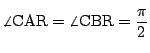 なので,
なので,
![]() となり,四点
となり,四点
![]() は同一円周上にあるからである.他も同様.
は同一円周上にあるからである.他も同様.
D'は六角形
AQCPBR の内部にあり,
したがって
![]() の外接円の内部にある.
円弧
AD'B は
の外接円の内部にある.
円弧
AD'B は
![]() の外接円の内部に含まれる.
の外接円の内部に含まれる.
![]() が
が ![]() 上にあるようになったときは,
逆に円弧
ACB が
上にあるようになったときは,
逆に円弧
ACB が
![]() の外接円の内部に含まれる.
の外接円の内部に含まれる.
![]() の動きに対して二つの円は連続的に変化するから,途中で二つの円が一致するときがある.
つまり,四点が同一円周上にあるときが存在する.
の動きに対して二つの円は連続的に変化するから,途中で二つの円が一致するときがある.
つまり,四点が同一円周上にあるときが存在する.
※ 京大では,99年後期にも同様な存在証明が出されている.『高校数学の方法』「条件の中に存在の根拠を見出す」の「存在の論証−中間値の定理 」.そこでは三通りの方法を証明したが,本問はそのうちの解3 と同じ連続関数の中間値の定理を根拠にする解である.99年後期の問題では可能であった直接作ってみせる方法が本問でもできるといいのだが.誰か挑戦してみてほしい.