次: 5. 上: 2. 解答 前: 3.

4.

n=1 のとき． f(x)=x+b とおく． f(q₁)=q₁+bでf(q₁)が有理数なので， b=f(q₁)-q₁ も有理数である．

n=m のとき成立するとする．

n=m+1 のとき． f(x) を x^m+1 の係数が1である x の m+1 次式とし， 相異なる m+1 個の有理数 $q_1,\ q_2,\ \cdots,\ q_{m+1}$に対し $f(q_1),\ f(q_2),\ \cdots,\ f(q_{m+1})$がすべて有理数であるとする．

因数定理より

$$f(x)=(x-q_{m+1})Q(x)+f(q_{m+1}) \quad \cdots\maru{1}$$

となる．ここで Q(x) は m 次式で x^m の係数は両辺の係数を比較して1である．

$q_1,\ q_2,\ \cdots,\ q_{m+1}$はすべて異なるので， $q_1,\ q_2,\ \cdots,\ q_m$に対し

$$Q(q_i)=\dfrac{f(q_i)-f(q_{m+1})}{q_i-q_{m+1}}$$

したがって $Q(q_1),\ \cdots,\ Q(q_m)$ はすべて有理数である．

数学的帰納法の仮定から Q(x) は有理数係数の多項式である．ゆえに$\maru{1}$から f(x) も 有理数係数の多項式である．

したがって題意が示された．

※別解　この問題は数学的帰納法を使うことなく解ける．

g(x)=f(x)-xⁿ は n-1 次式である． $g(q_1),\ g(q_2),\ \cdots,\ g(q_n)$もすべて有理数である．

n-1 次式 g(x) に対してn 個のxに対する値が定まれば g(x) は一意に定まる． 実際

$$\begin{eqnarray*}G(x)&=&g(q_1) \dfrac{(x-q_2)(x-q_3) \cdots (x-q_n)}{(q_1-q_2)... ...\cdots (x-q_{n-1})}{(q_n-q_1)(q_n-q_2) \cdots (q_n-q_{n-1})} \end{eqnarray*}$$

とおく．このとき $G(q_1)=g(q_1),\cdots,\ G(q_n)=g(q_n)$ なので恒等式の原理より G(x)=g(x) ． したがって

$$\begin{eqnarray*}f(x)&=&x^n+g(x)\\ &=&x^n+g(q_1) \dfrac{(x-q_2)(x-q_3) \cdots ... ...\cdots (x-q_{n-1})}{(q_n-q_1)(q_n-q_2) \cdots (q_n-q_{n-1})} \end{eqnarray*}$$

これから f(x) が有理数係数の n 次多項式であることが示された．

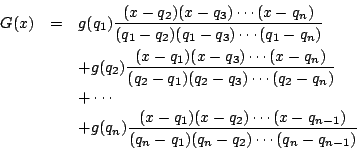
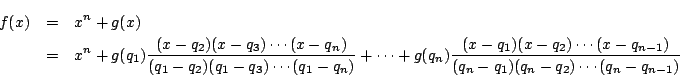
これが「ラグランジュの補間公式」の方法である．

これを勉強していた人は，「数学的帰納法で」という指示がかえって煩わしかったかも知れない．