点![]() から中心を通り直径
から中心を通り直径![]() を引く.
また点
を引く.
また点![]() から直線
から直線![]() への垂線の足を
への垂線の足を![]() とする.
円の中心
とする.
円の中心![]() から弦
から弦![]() に下ろした垂線を
に下ろした垂線を
![]() ,直線
,直線![]() と円の交点を
と円の交点を![]() とする.
このとき
とする.
このとき
![]() なので
なので
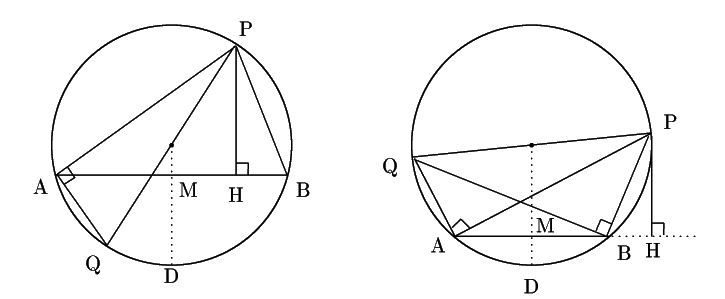
点![]() から直線
から直線![]() への垂線の足
への垂線の足![]() が
線分
が
線分![]() 上にないとき(図右).
円周角の相等から
上にないとき(図右).
円周角の相等から
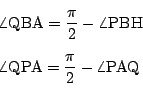
これを満たす点![]() は,
は,
![]() なら,左図の点
なら,左図の点
![]() .
.
![]() なら,右図の点
なら,右図の点
![]() .
.
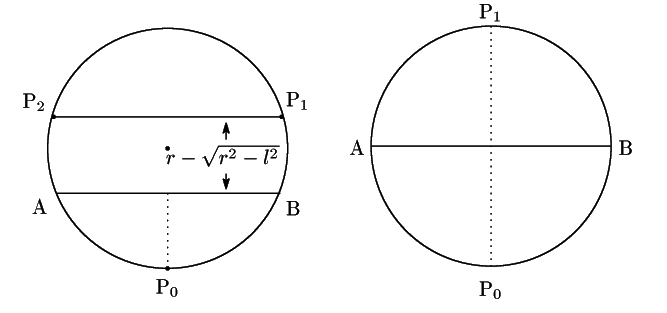
解2
![]() は弦の長さなので
は弦の長さなので![]() .ゆえにまた
.ゆえにまた
![]() である.
よって点
である.
よって点![]() は点
は点
![]() ではあり得ない.
ではあり得ない.
![]() とおく.
とおく.
また,円の中心![]() から弦
から弦![]() に下ろした垂線を
に下ろした垂線を
![]() ,直線
,直線![]() と円の交点を
と円の交点を![]() とする.
とする.
![]() なので
なので
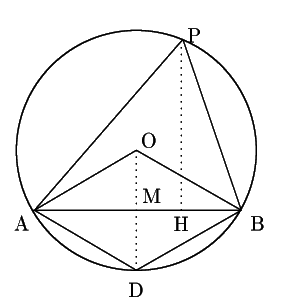
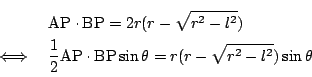
これを満たす点![]() は,
は,
![]() なら,左図の点
なら,左図の点
![]() .
.
![]() なら,右図の点
なら,右図の点
![]() .
(図略)
.
(図略)