2008�N���C��w���Łw��͊�b�x�𐧍삵���D����́C�����̒�`����͂��߂Ĕ����������̊�b�܂ł����Ȋ����I�ɏ������C���̏�ŁC�^������������ȉ~�O�����Ƃ���܂ŁC�����̊w�K�L�^�Ƃ��ď��������̂ł���D���݂̍��Z��̘͂_�̑g�ݗ��Ăɋ^���������������w�����C�����������čl���邽�߂̍ޗ��ɂ������Ƃ������Ƃ����@�ł������D
����ɑ��āC2011�N��3���C��w3�N����Y���烁�[���������������D
�l�́A���w�������w�Ȃ̂R�ł��B��w�����w�Ȃ̗l�X�ȋL����ǂ܂��Ă��������A�S���犴�����܂����B�{���ɂ��肪�Ƃ��������܂��B���ł����Ɋ��������̂��A�u��͊�b�v�̋L���ł��B�l�͕����w�Ȃł����A���w�ɔ��ɋ���������A���w�Ȃ̎��Ƃ����낢��Ɨ��C���Ă��܂��B��N�A�u���x�[�O�ϕ��v�̎��Ƃ���u���܂����B�������A�P�ʂ͂Ƃꂽ���̂́A���������Ƃ͑S�������Ȃ���Ԃł����B��̓I�ɂ͎��̂悤�ȋ^�₪�c��܂����B
�����x�̂����������낢�날���ĔώG������B�{���͂ǂꂩ�B
�����[�}���ϕ��Ő��藧���Ȃ����Ƃ����x�[�O�ϕ��Ő��藧�̂͂Ȃ����B
�����n���ƒ�ϕ��͂ǂ̂悤�Ɍ��ѕt���̂��ȂǂȂǂł��B
���낢��ȃ��x�[�O�ϕ��̖{��ǂ݂܂������������肷�邱�Ƃ͂���܂���ł����B������������߂��ɕ��𑱂��Ă���ƌ��ǁA
���ʐρi���x�j�͂ǂ̂悤�ɒ�`�����̂��B
�������̋t���Z���Ȃ��A��ϕ��Ɗ֘A����̂��B
�������킩���Ă��Ȃ��̂��ƋC�t���܂����B����ȂƂ��A�C���^�[�l�b�g�Ő�w���̋L�����������̂ł��B�����ŁA�u��ϕ��͔����Ƃ͓Ɨ��ɒ�`�������́v�Ƃ����A�l�ɂƂ��Ċv���I�ȋL���ɏo��܂����B�����Ɖ������ŗ܂��o�܂���(��)�B
�m���ɁA���Z���w�ł́A��ϕ������n���̍��Œ�`���Ă��܂��B������A���n�������݂��邩�ǂ����Ȃ�čl���������ɁA��ϕ����v�Z���܂��B�l�����̈�l�ł����B���̂��Ƃ��A���x�[�O�ϕ����킩��Ȃ��������{�̌����������̂ł��B�v�Z���@�̏K�������ō������킩��Ȃ���A��͂�ǂ����ŕ��Q���o�Ă���̂ł��ˁB
�����C�����̐��w���t�̓��[�}���a�̊T�O����m�炸�C��ϕ��̒�`���������Ă͋����Ȃ��D���Z���̑����́C��ϕ��̒�`���ӎ����Ă͐g�ɂ��Ȃ��D����ł������Ȃ���u��`����v�Ƃ������ƂɎ��o�I�ł��鍂�Z���͂���D������ɂ��C����ɓ������鋳��łȂ���Ȃ�Ȃ��D�Ƃ��낪�C�ނ炪��ϕ��̒�`�����ȏ��̒ʂ�ɗ�������C��w���w�Ɩ����𗈂��D
���[���̔ނ́C�Ƃɂ������͂œ��{�̍��Z���w�����z�����D���ꂪ�ł��Ȃ��āC���ƂȂ����������ƞB�������c�����܂܂̊w�����������낤�D����ł͕�����킸�{���̊�b�I�Ȍ����͂ł��Ȃ��̂ł͂Ȃ����D�傫�Ȗ��ł���D
![]() 1965�N���ȏ��i�����o�Łj��I�CIIB�D
1965�N���ȏ��i�����o�Łj��I�CIIB�D
![]() 1969�N���ȏ��i���{���@�j��I�CIIB�CIII�D
1969�N���ȏ��i���{���@�j��I�CIIB�CIII�D
![]() 1982�N���V�W�i�Ȋw�V���Ёj�̐��wI�C�㐔�E�C��b��́C�����E�ϕ��D
1982�N���V�W�i�Ȋw�V���Ёj�̐��wI�C�㐔�E�C��b��́C�����E�ϕ��D
![]() 1997�N���ȏ��i�����o�Łj��I�CA�CII�CB�CIII�CC�D
1997�N���ȏ��i�����o�Łj��I�CA�CII�CB�CIII�CC�D
![]() 2005�N���ȏ��i�����o�Łj�̈ꕔ�ʂ��D
2005�N���ȏ��i�����o�Łj�̈ꕔ�ʂ��D
![]() 2014�N���ȏ��i�����o�ŁC�[�ъفC�������ЁjI�CA�CII�CB�CIII�D
2014�N���ȏ��i�����o�ŁC�[�ъفC�������ЁjI�CA�CII�CB�CIII�D
�ʐς̒�`���C�������`�ɂ�������̋ߎ��C����т��̋Ɍ��Ƃ��ĂȂ����D���̏�ŁC���̃O���t�ň͂܂��̈�̖ʐς��敪���ςɂ���ĂȂ���C����܂��ċ�Ԃ�![]() �����������[�}���a
�����������[�}���a
 �̋Ɍ��ɂ���Ē�ϕ�����`�����D���̒�`�ɂ��ƂÂ��āC��ϕ������n���̒l�̍��ƈ�v���邱�Ƃ��ؖ������D
�̋Ɍ��ɂ���Ē�ϕ�����`�����D���̒�`�ɂ��ƂÂ��āC��ϕ������n���̒l�̍��ƈ�v���邱�Ƃ��ؖ������D
���wIII�ł́C�u�����@�v�ɂ����āC�A�����̍ő�l�ƍŏ��l�̑��݂������ɁC���[���̒藝���o�R���ĕ��ϒl�̒藝���ؖ������D�����ĘA�����̍ő�l�ƍŏ��l�̑��݂́u�m���Ă���v�Ɩ��L�����D
��ϕ��́C�C�ӂ̏���Ԃɂ��Ẵ��[�}���a�̋Ɍ��Œ�`�����D�����Ē�ϕ��̕��ϒl�̒藝��p���āC�A�����ɑ��āC�ϕ��@�͔����@�̋t���Z�ł��邱�Ƃ������Ă���D
���wII�Ŗʐς�����`�ɗp�����C���̃O���t��![]() ���ň͂܂��̈�̖ʐς��C
���ň͂܂��̈�̖ʐς��C![]() �����Ŕ�������Ƃ��Ƃ̊��ɂȂ邱�Ƃ��������D�ʐς̔�����
�����Ŕ�������Ƃ��Ƃ̊��ɂȂ邱�Ƃ��������D�ʐς̔�����![]() �ƂȂ邱�Ƃ𐔊wII�Ŏ����D�����Ă�������n�������݂��鍪���ɗp���āC��ϕ������n���̒l�̍��Œ�`�����D�܂�C�ϕ����C������O��Ƃ��Ē�`�����D���̒�ϕ��̒�`�́C���wIII�ł��ς��Ȃ��D
�ƂȂ邱�Ƃ𐔊wII�Ŏ����D�����Ă�������n�������݂��鍪���ɗp���āC��ϕ������n���̒l�̍��Œ�`�����D�܂�C�ϕ����C������O��Ƃ��Ē�`�����D���̒�ϕ��̒�`�́C���wIII�ł��ς��Ȃ��D
����C��ϕ��Ɋւ��āC2014�N�łł͎��̂悤�ȋL�q�������D
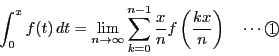
���j�I�ɂ́C��ϕ��͇@�Œ�`���ꂽ�D
���ȏ��̒��҂́C���̋L�q�ŁC�{�����ꂪ��ϕ��̒�`�ł���Ƃ������Ƃ��������������̂����m��Ȃ��D�������C���̋��ȏ��̕��ʂ���́C���Ă͂��̂悤�ɒ�`����Ă��������͈Ⴄ�C�ƌ�������Ƃ����Z���ɓ`���D���邢�́C���n���̒l�̍��Ƃ��Ē�`���錻�s�̒�`�̕�����������`�ł���ƍ��Z�����������D
�܂��C2014�N�łł́C�ʐς����[�}���a�ŕ\�����Ƃ͔��W�I����̒��ŕ�������D�Ƃ��낪���̋L�q���Ȃ����D
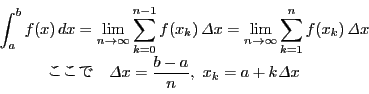
��ϕ����C��̂悤�Șa�̋Ɍ��Ƃ��ċ��߂邱�Ƃ��C ��ϕ����敪���ϖ@�Ƃ����B
�܂��C�u���ρv�Ƃ́w��͊T�_�x�̑�3�͖`���u28�@�Ñ�̋��ϖ@�v�ɂ���悤�ɁC��т��Ėʐς�̐ς����߂邱�Ƃł������D�Ƃ��낪�����ł͒�ϕ������߂邱�ƂƂ���Ă���D����ɂ܂��C�u��ϕ���a�̋Ɍ��Ƃ��ċ��߂�v�Ə�����Ă��邪�C��͊w�̗���ł����C����͉E�ӂ̘a�̋Ɍ������ӂ̒�ϕ��̒�`�Ȃ̂ł����āC������瑼�������߂�Ƃ������Ƃł͂Ȃ��D
����ɁC���ۂɍ��Z������邱�Ƃ́C�����Ă܂����̋��ȏ��̗��ɂ����邱�Ƃ́u����̘a�̋Ɍ����ϕ��Ōv�Z����v���Ƃł���C���̋L�q�Ƃ͋t�ł���D������܂��߂ɓǂ��Z���́C�傫���������邾�낤�D
2014�N�́u�K�C�v�̕����Ɂu���W�v���q�����Ƃ������ʁC�L�q�̓��ꐫ�������Ă���D
�ȏ�A�e����̋��ȏ��̓����_���������D1997�N�ȍ~�C���[�}���a���ϕ��̒�`�Ƃ��邱�Ƃ�����C�����@��O��ɒ�ϕ������n���̒l�̍��Œ�`���Ă���D�����Ɍ��s�̓��{�̍��Z���ȏ��̓���������D���̌��ʁC�u�����@�Ɛϕ��@�݂͌��ɓƗ��ɒ�`����C���ꂪ�݂��ɋt�̕��@�ł���v�Ƃ�����{�藝�̈Ӌ`���B����C�L�q�͂��܂��܂̖����⓰�X�߂�����J�肩������������D
��͊w�̕��@�͒P�������Ȃ��̂ŗ͋����D���ׂĂ������_�ɍ����Â��邱�Ƃ��ł���D�Ƃ��낪�C���{�̍��Z��͂̋��ȏ��́C���_�\�����ώG�ŗ͋����������Ă���D�_�q�����o�I�ȉ���ɗ����Ė��肪�������鍪����₤���Ƃ������ւ�ア�D���̂��ߗ���������ׂ��n�_���������C�悯���ɗ���������ɂȂ��Ă���D
���ۂɑ����̐���̒��ŋ��ȏ������鍢��͗�������D�������C��w���N���̉�͊w�Ɩ��������ɂȂ���悤�ɂ��Ȃ���Ȃ�Ȃ��D�����I�̋��ȏ��̕ω��́C���{�̉Ȋw����̍����Ɛ��ނ��ے����Ă���D���̊ԁC���{�̍��Z�ł̔����@�E�ϕ��@�͐��ނ������Ă����D���̂悤�Ȃ��Ƃł́C�܂��܂��Ȋw���ꂪ�i�݁C��҂̍l����͂������Ă����D
![]() �̂Ƃ��C
2��������
�̂Ƃ��C
2��������![]() �͑��قȂ�2�̎���
�͑��قȂ�2�̎���
 �����D
����āC�Ȑ�
�����D
����āC�Ȑ�![]() ��
��![]() ���ƈقȂ�2�_�Ō����D
���ƈقȂ�2�_�Ō����D
![]() �̂Ƃ��C�Ȑ�
�̂Ƃ��C�Ȑ�![]() �̒��_
�̒��_
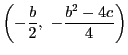 ��
��
![]() ���̉����ɂ���C�Ȑ���
���̉����ɂ���C�Ȑ���![]() ���ƈقȂ�2�_�Ō����D
����āC2��������
���ƈقȂ�2�_�Ō����D
����āC2��������![]() �͑��قȂ�2�̎����������D
�͑��قȂ�2�̎����������D
���Ƃ�肱��2����͓��l�ł���C�܂��㐔�������̍��̑��݂��̈�ɂ�����A�����̍ő�l�ŏ��l�̑��ݒ藝���玦�����̂ł��邩��C�����ꂪ����{�I�ł���̂��́C���_�̒i�K�ɂ��D
�������C����I�ɂ́C���݂������ɂ͂��̍������K�v�ł��邱�Ƃ������Ȃ���Ȃ�Ȃ��D�Ƃ��낪�u�Ȃ���_�����݂���Ƃ�����̂��D���̍����͉����v�Ɩ₤���Ƃ͋������C��_�̑��݂����o�I�ɗ������ďI���D���̕����ɕς�����D
�A�����̒��Ԓl�̒藝���C1980�N��̔����E�ϕ��ł͂��߂Č����D�������������獪���Ƃ��Ă̎����̘A�����ɂ͂ӂ��ꂸ�C���̌��ʁC��w�ł̐��w�ɂ͂Ȃ���Ȃ��D
���Z�ł͍��̑��݂������Ɍ�_�̑��݂������C�A�����̊�{�����̖����܂ł����Z�ł����Ȃ��C��w���w�ł́C�����_����_�܂��đ㐔�������̍��̑��ݒ藝�������D���̂悤�ɍ��Z���w�����w���w�ւ̔��W���Ȃ���˂Ȃ�Ȃ��D
�Ȃ����̂悤�Ȃ��Ƃ��N�������̂��D���̔w�i�͉����D�傫�������C�ߑ���{���̂��̂����m�̌��ʂ���e����̂ɖZ�����C������₤�]�T���Ȃ������Ƃ������Ƃ�����D���̂Ȃ��ł���ɁC1970�N��ɍ��Ƃ̋���v�z�ɂ����ē]�����������D
���́C1973�N�H�ɋ����ɂȂ����D���ꂩ��\���N�Ԃ̐E���n��ł̎d����ʂ��āC���̂悤�ȋ���ς������Ƃ��ł����D
����Ƃ͐l���̂��̂���Ă邱�Ƃł���D��l��l��l�ԂƂ��Ĉ�Ă�D��l��l�̐l�Ԃ��J�Ԃ�����D�������Č��ꂽ�l�Ԃ̂��܂��܂ȗ͂́C�������Čl�̎����ł͂Ȃ��D�ǂ�ȗ͂������̐l�X�Ɉ͂܂��܂�Ă͂��߂ĊJ�Ԃ���D�ł��邩��C��܂ꂽ����̗͂��C��ĂĂ��ꂽ���̐��ԂɕԂ��Ȃ���Ȃ�Ȃ��D�����ł����ɏz�����Ă䂩�Ȃ���Ȃ�Ȃ��D�������Đl����āC�l�Ɏx�����鐢�łȂ���Ȃ�Ȃ��D���Â��Ƃ��̂悤�Ɏv���D
�Ƃ��낪�������C���{�̋���͑傫�ȓ]�����͂��߂Ă����D��������R�c���1970�N��u�l�I�����̊J���v�Ƃ������Ƃ������͂��߁C����͍����ɑ����Ă���D�u�l�I�����v�Ƃ͐��Y�����ɕK�v�ȘJ���͂Ƃ������Ƃł���D�l��l�Ƃ��Ĉ�Ă鋳�炩��C�l�������Ƃ��Ďg����悤�ɂ��鋳��ւ̓]���ł���D���̔\�͂��J������̂����炾�Ƃ����킯�ł���D����Y�����̈ꕔ�Ƃ���l�������\�ʉ�����D
���Ƃ��ߑ�̊w�Z���x�́C�Y�ƋZ�p���K�������l�Ԃ̈琬��ړI�ɂ��Ă���D���̎���̕����Ƃ�����x����Z�p���K������ꂪ����@�ւł��邱�Ƃ͕K�R�ł���D�܂��C�l�Ԃ����炩�̐��Y�ɂȂ��邱�Ƃ́C�l�ԂƂ��Ă̑��ݏ������̂��̂ł���D������d�������߂�l���ׂĂɎd����ۏႷ��D�J������ۏႷ��D���ꂪ�l�Ԃ̑������d��Ƃ������Ƃ��D���������̂��Ƃ́C�l�Ԃ����Y�̎����ł���Ƃ������Ƃ��Ӗ�����̂ł͂Ȃ��D
�l�I�����Ƃ����ϓ_����������邱�ƂŁC������₢�C���@���̂��̂��l��������C��߂�ꂽ���@�ɂ���Đ��m�Ɍv�Z�ł���悤�ɂ���C�Ƃ��������ɐ��w����v�z���ς�����D������₤�ᔻ���_���C�����I�����ɂ�錻��m����d�����鋳��ւ̓]���ł���D���ꂪ���̎��Ԃ��o�ċ��猻��ɓ`���C�����ċ��ȏ����ς���Ă����D���̕������́C�E��Ƃ�ƌ�����2012�N�ȍ~���ς���Ă��Ȃ��D
���Ȃ݂ɁC�������������Z�͂���������̒�ӍZ�ł������D���̂Ȃ��Œn��̂��ׂĂ̎q�ǂ��ɍ��Z�����ۏႵ�C������͂����悤�Ƃ���Ă����D���k���u�킩����Ɓv��v�����C����������ɉ����悤�Ƃ��Ă����D�������C���̂悤�ȍ��Z���Ƃ�܂��Љ�̕ϓ]�̒��ŁC���ɔp�Z�ɂȂ����D���w��������Z������Ă��ꂽ�E��ł������D
��w�ɂ����āC��ʋ��{�ے����Ȃ��Ȃ�C����������ے��ɓ���悤�ɂȂ����̂��C�����l�I�����Ƃ����ϓ_���w�i�ɂ���̂ł͂Ȃ����낤���D
����������ł́C�{���ɉ����Ƃ���[���l���C�V���Șg�g�݂����悤�Ȑl�Ԃ͈炽�Ȃ��D����͐�̃��[���������Ă���D�ߔN�C���{�̎Y�Ƃ���n���������C�������̕���ł͌����̐��ނ��N�����Ă���D����́C�l�Ԃ������Ƃ݂Ȃ��l���������݂��������̂ł���D�����ɁC������{�̎Y�Ƃ��n���������������{����������D
�l�Ԃ͎����ł͂Ȃ��D�l���̂��̂Ƃ��āC�܂��߂ɓ����C���̂��ɂ��C�אl�����C�����Ƃ���������́C�������ɏ��������Đ����Ă䂭�D�ЂƂ�ЂƂ�̗͂͌l�̂��̂ł͂Ȃ��C�݂��̂��̂ł���D���ꂪ�l�ԂƂ������̂��D���̂Ƃ��o�ς͐l�ԂɂƂ��ĖړI�ł͂Ȃ��D�����܂ŕ��@�ł����i�ł���D���������l�Ԃ���ĂȂ���Ȃ�Ȃ��D