実は射影平面はユークリッド平面を部分概念として含むより広い概念と見なすことができる.ユークリッド平面を基礎に,同値類の考え方を用いて,その一般化を構成する,これがパスカルの思想の内にあることであった.このようにして射影平面が現実に構成できることを確認することはたいへん重要である.
パスカルはユークリッド平面の直線の集合に関して「束」を定義する.直線の集合が束であるとは,各直線がすべて同じ点を通るかまたはすべて平行である,こととする.これを基礎にしよう.
![]() をユークリッド平面の相異なる2直線の組
をユークリッド平面の相異なる2直線の組![]() の集合とする.
の集合とする.

この同値関係による![]() の商
の商![]() を射影平面という.これを
を射影平面という.これを![]() と書こう.
と書こう.![]() の各要素は同値類であるが,これをユークリッド平面の2直線の組
の各要素は同値類であるが,これをユークリッド平面の2直線の組![]() で定まる射影平面
で定まる射影平面![]() の「点」ともいう.ユークリッド平面において平行でない2直線の組
の「点」ともいう.ユークリッド平面において平行でない2直線の組![]() で定まる射影平面
で定まる射影平面![]() の点は,ユークリッド平面の1点と対応する.
の点は,ユークリッド平面の1点と対応する.
平行な2直線![]() によって定まる射影平面
によって定まる射影平面![]() の点には対応するユークリッド平面は存在しない.この点を無限遠点と呼ぼう.平行な直線の組は無限遠点を定め,同じ平行でも方向の異なる組は,異なる無限遠点を定める.こうして射影平面
の点には対応するユークリッド平面は存在しない.この点を無限遠点と呼ぼう.平行な直線の組は無限遠点を定め,同じ平行でも方向の異なる組は,異なる無限遠点を定める.こうして射影平面![]() は,ユークリッド平面にそれら無限遠点を加えたものと考えることができる.
は,ユークリッド平面にそれら無限遠点を加えたものと考えることができる.
次に![]() に直線を定義する.直線は
に直線を定義する.直線は![]() の2つの要素
の2つの要素![]() と
と![]() の組を基礎に定義される.ユークリッド平面でも,直線
の組を基礎に定義される.ユークリッド平面でも,直線![]() の上にある他の点
の上にある他の点![]() をとると直線
をとると直線![]() は直線
は直線![]() と一致する.
と一致する.![]() の2つの要素
の2つの要素![]() と
と![]() の組がどのようなときに同じものを定めるのか.この同値関係を定めねばならない.
の組がどのようなときに同じものを定めるのか.この同値関係を定めねばならない.
さてわれわれの構成では,
![]() は束の集合であり,
その要素
は束の集合であり,
その要素![]() とは2直線の組を「同じ束を定めるなら同値」という関係で類別したものである.
要素
とは2直線の組を「同じ束を定めるなら同値」という関係で類別したものである.
要素![]() に対して,
に対して,![]() を定める2直線の組を一つとるとき,
その2直線を「
を定める2直線の組を一つとるとき,
その2直線を「![]() の2直線」と略記する.
の2直線」と略記する.
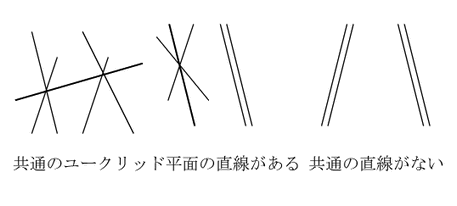
![]() ,
,![]() ともユークリッド平面の点に対応していればそれらの点を通る直線がただ一つ存在する.
ともユークリッド平面の点に対応していればそれらの点を通る直線がただ一つ存在する.
![]() がユークリッド平面の点に対応し
がユークリッド平面の点に対応し![]() が平行2直線の束であれば,
が平行2直線の束であれば,
![]() で定まる点を通り
で定まる点を通り![]() の直線と平行な直線がただ一つ存在し,
これが双方と束をなす.
の直線と平行な直線がただ一つ存在し,
これが双方と束をなす.
![]() ,
,![]() ともユークリッド平面の平行2直線の束であれば,
ともユークリッド平面の平行2直線の束であれば,
![]() の異なる2点なので,双方に平行な直線は存在しない.
□
の異なる2点なので,双方に平行な直線は存在しない.
□
![]() の要素の組の集合を
の要素の組の集合を![]() とする.
とする.
![]() は次のいずれかが成り立つことである.
は次のいずれかが成り立つことである.
![]() かつ
かつ
![]() とする.
とする.
![]() の2直線とも
の2直線とも![]() の2直線とも束をなすユークリッド平面の直線があり,
の2直線とも束をなすユークリッド平面の直線があり,
![]() の2直線とも
の2直線とも![]() の2直線とも束をなすユークリッド平面の直線があり,
それが一致する場合.
の2直線とも束をなすユークリッド平面の直線があり,
それが一致する場合.
![]() の2直線とも
の2直線とも![]() の2直線とも束をなすユークリッド平面の直線があり,
の2直線とも束をなすユークリッド平面の直線があり,
![]() の2直線とも
の2直線とも![]() の2直線とも束をなすユークリッド平面の直線があり,
それが一致するので,
の2直線とも束をなすユークリッド平面の直線があり,
それが一致するので,
![]() の2直線とも
の2直線とも![]() の2直線とも束をなすユークリッド平面の直線があり,
の2直線とも束をなすユークリッド平面の直線があり,
![]() の2直線とも
の2直線とも![]() の2直線とも束をなすユークリッド平面の直線があり,
それが一致する.
の2直線とも束をなすユークリッド平面の直線があり,
それが一致する.
ないときも同様である. □
この同値関係による![]() の商
の商![]() の各要素を
の各要素を![]() の直線という.直線
の直線という.直線![]() で
で![]() の2直線とも
の2直線とも![]() の2直線とも束をなすユークリッド平面の直線が存在する場合,それはただ一つである.
の2直線とも束をなすユークリッド平面の直線が存在する場合,それはただ一つである.![]() の2直線とも
の2直線とも![]() の2直線とも束をなすユークリッド平面の直線が存在しない場合は,そのような直線はすべて同値であるから,それによって商
の2直線とも束をなすユークリッド平面の直線が存在しない場合は,そのような直線はすべて同値であるから,それによって商![]() の要素がただ一つ定まる.その直線を「無限遠直線」と名づけると,
の要素がただ一つ定まる.その直線を「無限遠直線」と名づけると,![]() から無限遠直線を除いた集合と,ユークリッド平面の直線の間に一対一対応が成り立つ.
から無限遠直線を除いた集合と,ユークリッド平面の直線の間に一対一対応が成り立つ.
![]() の点
の点![]() と直線
と直線![]() に対して,
に対して,![]() が直線
が直線![]() 上にあるとは,
上にあるとは,
点![]() も2直線
も2直線![]() 上にも
上にも![]() 上にもあるとする.
点
上にもあるとする.
点![]() は
は![]() 上にもあるので
上にもあるので
![]() .これから
.これから
![]() である.同様に
である.同様に
![]() となり
この結果
となり
この結果
![]() .異なる2直線であるという仮定に反する.
.異なる2直線であるという仮定に反する.
第2の場合.
![]() の2直線とも
の2直線とも![]() の2直線とも束をなすユークリッド平面の直線を
の2直線とも束をなすユークリッド平面の直線を![]() とし,
とし,
![]() と平行な直線を
と平行な直線を![]() とする.
とする.![]() で定まる
で定まる![]() の点を
の点を
![]() とする.
とする.![]() 自身は
自身は![]() の2直線とも
の2直線とも![]() の2直線とも束をなすので
の2直線とも束をなすので
![]() である.
である.
![]() の2直線は
の2直線は![]() の2直線と束をなすか,
の2直線と束をなすか,![]() の2直線と束をなすか,
いずれとも束をなさないかのいずれかである.
の2直線と束をなすか,
いずれとも束をなさないかのいずれかである.
![]() の2直線は
の2直線は![]() の2直線と束をなすか,
の2直線と束をなすか,![]() の2直線と束をなすなら
の2直線と束をなすなら
![]() か
か![]() である.
いずれとも束をなさないなら,
である.
いずれとも束をなさないなら,
![]() の2直線とも
の2直線とも![]() の2直線とも束をなすユークリッド平面の直線がなく,
の2直線とも束をなすユークリッド平面の直線がなく,
![]() の2直線とも
の2直線とも![]() の2直線とも束をなすユークリッド平面の直線がない,
ことが成り立ち,
の2直線とも束をなすユークリッド平面の直線がない,
ことが成り立ち,
![]() である.
である.
よって点![]() は2直線
は2直線![]() 上にも
上にも![]() 上にもある.
ただ一つであることは,第1の場合と同様に成り立つ.
□
上にもある.
ただ一つであることは,第1の場合と同様に成り立つ.
□
かくして,射影平面![]() とそのうえの直線の集合
とそのうえの直線の集合![]() で2点は1直線を定め,2直線は1点を定めるものを構成した.
で2点は1直線を定め,2直線は1点を定めるものを構成した.![]() においては,ユークリッド平面の点に対応する点も対応しないいわゆる無限遠点もまったく同等であり,またユークリッド平面の点に対応する直線も無限遠直線もまったく同等であって,たいへん単純な構造になっている.
においては,ユークリッド平面の点に対応する点も対応しないいわゆる無限遠点もまったく同等であり,またユークリッド平面の点に対応する直線も無限遠直線もまったく同等であって,たいへん単純な構造になっている.
射影平面![]() は同じ線束が定めるものを射影平面の点とすることで得られた.その基礎になっているのはユークリッド平面であり,さらにその土台には連続性をもつ実数体がある.2点が1直線を定め,2直線が1点を定める.こうして実数体に土台をもつ射影平面の存在が確認された.
は同じ線束が定めるものを射影平面の点とすることで得られた.その基礎になっているのはユークリッド平面であり,さらにその土台には連続性をもつ実数体がある.2点が1直線を定め,2直線が1点を定める.こうして実数体に土台をもつ射影平面の存在が確認された.
さらにまた,この方法は自然に空間にある「平面束」の考え方を導く.1直線を共有するか,または互いに平行な平面の集合を束という.この束に同値関係を同様に自然に拡張された方法で定義し,その同値類を射影空間![]() とする.
とする.
しかしこれらの方法は,さらなる基本性質を同値類としての点や直線の定義にかえってなさねばならず,たいへん複雑である.ここから逆にどれだけの公理があれば,射影幾何の本質をとらえられるのかという問いが浮かびあがる.これは19世紀から20世紀にかけての時代に深く研究された.