![]() に4直線
に4直線
![]() が同一の部分平面
が同一の部分平面![]() の一般の位置にある.
この4直線とそれから定まる6交点
の一般の位置にある.
この4直線とそれから定まる6交点
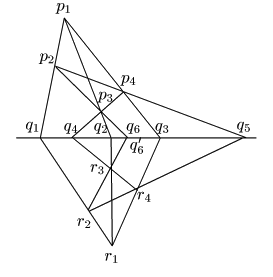
![]() からなる図形を完全四辺形という.この6点を頂点ともいう.
■
からなる図形を完全四辺形という.この6点を頂点ともいう.
■
![]() に4直線
に4直線
![]() が同一の部分平面
が同一の部分平面![]() の一般の位置にある.
この4直線とそれから定まる6交点
の一般の位置にある.
この4直線とそれから定まる6交点
![]() からなる図形を完全四辺形という.この6点を頂点ともいう.
■
からなる図形を完全四辺形という.この6点を頂点ともいう.
■
辺といってもユークリッド幾何の線分としての辺ではない. 射影幾何でいう辺は直線である.
直線![]() 上の6点
上の6点
![]() に対し,
完全四角形
に対し,
完全四角形![]() で,
その6直線
で,
その6直線
![]() ,
,
![]() と
と![]() の交点がこの順に
の交点がこの順に
![]() となるものが存在するとき,
この6点を四角性六点,または六点図形という.
となるものが存在するとき,
この6点を四角性六点,または六点図形という.
![]() おける双対概念を四辺性六辺,六辺図形という.
■
おける双対概念を四辺性六辺,六辺図形という.
■
 証明
直線
証明
直線![]() 上の異なる3点と,異なる2点を
上の異なる3点と,異なる2点を
![]() と
と![]() とする.
これが二つの四角形
とする.
これが二つの四角形
![]() と
と
![]() と
と![]() の交点であるとする.他の交点を
の交点であるとする.他の交点を![]() とする.
とする.
![]() と
と
![]() について
について
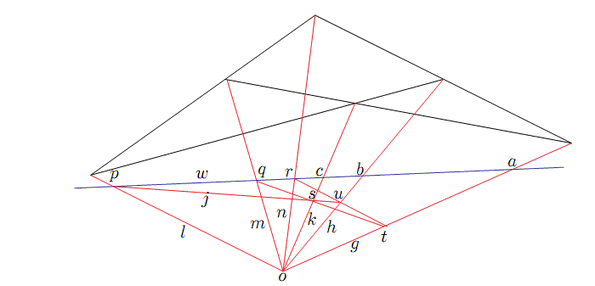
点![]() から直線
から直線![]() を引き,
を引き,![]() との交点を
との交点を![]() とする.
とする.
![]() と
と![]() を結ぶ.
その
を結ぶ.
その![]() との交点
との交点
![]() をとる.
また
をとる.
また![]() と
と![]() との交点を
との交点を![]() とする.
5直線
とする.
5直線
この結果
![]() は
4点
は
4点![]() に関する四角性六点である.
□
に関する四角性六点である.
□
直線である.これを直線上の
が四角性六点であるとする.
上にない点
とこれらを結ぶ直線を
とする.
は四辺性六辺である.
直線体はシュタウト(K.G.C.von Staudt,1798〜1867)が先鞭をつけた.複比を計量に依存しないで定義する,つまり複比を長さという概念から独立に定義することがその時代の一つの目標だった.シュタウトが抽象的に公理から定義された射影幾何において体が定義され,それによって一般射影座標が可能であることを示したのである.
もとより,指標となったのはユークリッド空間の直線で,ここに座標を導入すれば直線上の点の集合が実数体と同型になる,ということであった.これを公理から建設された射影幾何でも実現すること.これが当面の目標である.
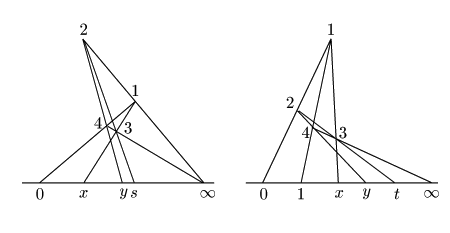
これがなぜ和と積になるのか.
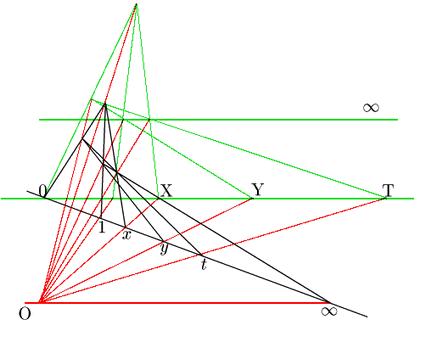
射影平面の一つのモデルは3次元ユークリッド空間の1点Oを通る直線の集合であった.
この直線の集合を,Oと![]() を結ぶ直線と平行な平面で切ると,ユークリッド平面が得られる.ここに移せば確かにユークリッド平面上の線分の長さの和が得られることを確認しよう.赤線は射影平面の要素としての直線.緑線はそれをOと
を結ぶ直線と平行な平面で切ると,ユークリッド平面が得られる.ここに移せば確かにユークリッド平面上の線分の長さの和が得られることを確認しよう.赤線は射影平面の要素としての直線.緑線はそれをOと![]() を結ぶ直線と平行で点
を結ぶ直線と平行で点![]() を通る平面で切った図形である.
を通る平面で切った図形である.
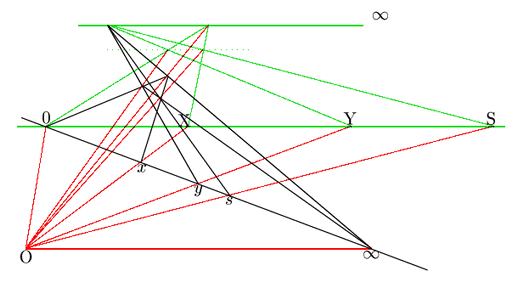 図からユークリッド平面上で対応する点を大文字で示す.
和について,
対応するユークリッド平面で
図からユークリッド平面上で対応する点を大文字で示す.
和について,
対応するユークリッド平面で
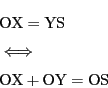
 積についても同様である.
対応するユークリッド平面で
積についても同様である.
対応するユークリッド平面で
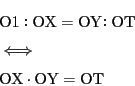
このように, 射影平面の直線上の点に関する和と積の定義は, ユークリッド平面で和と積を作図する方法を, 射影辺面に引き戻したものであり,自然である.
命題 44
![]() 上の
上の![]() を除く点は,上記演算に関して体となる.
加法の単位元は
を除く点は,上記演算に関して体となる.
加法の単位元は![]() ,乗法の単位元は
,乗法の単位元は![]() である.
この体を
である.
この体を
![]() と表し,辺
と表し,辺
![]() 上の直線体という.
■
上の直線体という.
■
証明 示すべきは
次の命題が成りたつ.
射影幾何![]() によって,その直線上の直線体がすべて同型で,
この同型を除いて体が一意に確定する.
この体
によって,その直線上の直線体がすべて同型で,
この同型を除いて体が一意に確定する.
この体![]() を射影幾何
を射影幾何![]() の係数体という.
直線体
の係数体という.
直線体
![]() は点の集合に体の構造を入れたものであり,
係数体
は点の集合に体の構造を入れたものであり,
係数体![]() は抽象的な体である.
は抽象的な体である.
証明
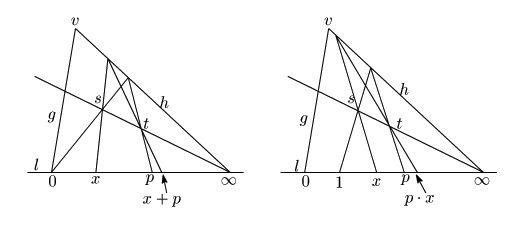
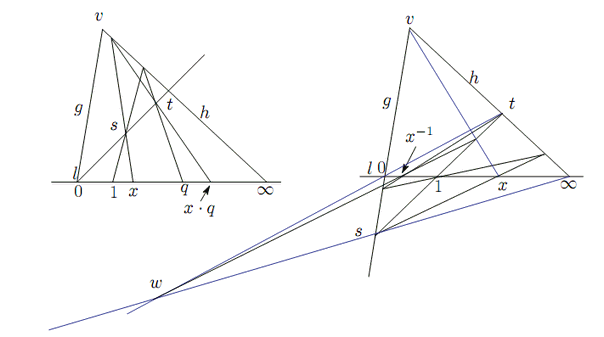
これはまた,![]() と
と![]() を入れかえ,
を入れかえ,![]() を動かさない射影写像を作り,それによって
を動かさない射影写像を作り,それによって![]() を移した先として
を移した先として![]() を定めてもよい.図の青線では
を定めてもよい.図の青線では![]() と
と![]() を中心とする二つの配景写像で入れかえを行い,それで
を中心とする二つの配景写像で入れかえを行い,それで![]() をうつしている.
□
をうつしている.
□
一方,命題46によって![]() ,
,![]() あるいは
あるいは![]() という直線体から同じ直線体への写像が,直線の射影写像から得られる.
という直線体から同じ直線体への写像が,直線の射影写像から得られる.
両命題とも,射影写像は同じ![]() で表されているが,
で表されているが,
![]() が導く体の同型と,
が導く体の同型と,![]() が直接に指定する体内部の対応は,別個のものである.
が直接に指定する体内部の対応は,別個のものである.
証明 命題46より 直線体
逆に枠
![]() を動かさない射影写像
を動かさない射影写像
![]() をとる.
をとる.
![]() の導く体
の導く体
![]() の同型が内部自己同型であることを示す.
の同型が内部自己同型であることを示す.
点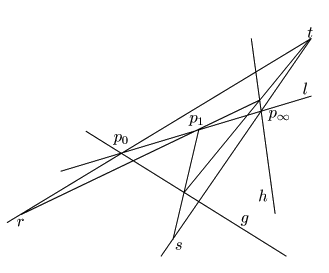 を通る
を通る![]() と異なる直線
と異なる直線![]() と
と![]() 平面上の
平面上の![]() や
や![]() に含まれない点
に含まれない点![]() をとる.
射影写像
をとる.
射影写像
![]() に定理5を適用すると,
2点
に定理5を適用すると,
2点![]() と直線
と直線![]() が存在して
が存在して
これらの直線や点に対して
命題46の(2)で定めた点![]() ,
(3)で定めた点
,
(3)で定めた点![]() をとると,
をとると,
第一は射影写像の単一性である.それは
2直線間の射影写像は3点の対応点を与えれば一意に定まる.という命題である.
第二はパップスの定理である.それは
同一平面上にある2直線上にそれぞれ相異なる3点である.をとれば, 3点
は共線である.
相異なる2直線![]() が点
が点![]() で交わっている.
で交わっている.
![]() から
から![]() への射影写像
への射影写像![]() が点
が点![]() を動かさないなら,
を動かさないなら,
![]() はある点を中心とする配景写像である.
■
はある点を中心とする配景写像である.
■
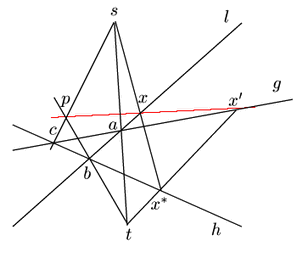 とする.
とする.
![]() とする.
とする.![]() なので
なので
![]() は共線である.
は共線である.![]() ,
,![]() とおく.
とおく.
![]() の任意の点
の任意の点![]() に対して
に対して
![]() ,
,
![]() とおく.3点の組
とおく.3点の組![]() と
と
![]() に関してパップスの定理を用いることにより
3点
に関してパップスの定理を用いることにより
3点
![]() は共線である.
よって
は共線である.
よって
![]() である.
□
である.
□
(1)![]() (2)
(1)が成りたつとする.
直線
(2)
(1)が成りたつとする.
直線![]() の直線体
の直線体
![]() が可換であれば,
直線
が可換であれば,
直線![]() 上の枠
上の枠
![]() を動かさない射影写像は恒等変換のみとなる.
直線
を動かさない射影写像は恒等変換のみとなる.
直線![]() から同一平面上の直線
から同一平面上の直線![]() への射影写像
への射影写像
![]() が
いずれも直線
が
いずれも直線![]() 上の枠
上の枠
![]() を
直線
を
直線![]() 上の枠
上の枠
![]() に写すとすると,
に写すとすると,
![]() は
直線
は
直線![]() 上の枠
上の枠
![]() を動かさない写像であり,恒等写像になる.
よって
を動かさない写像であり,恒等写像になる.
よって
![]() である.
である.
逆に(2)が成り立つとする.
枠
![]() を動かさない
を動かさない![]() から
から![]() への射影写像で恒等写像でないもの
への射影写像で恒等写像でないもの![]() があれば,
直線
があれば,
直線![]() から直線
から直線![]() への射影写像
への射影写像![]() に対し
に対し
![]() も
直線
も
直線![]() から直線
から直線![]() への射影写像で異なる.
これは単一性に反するので,直線体の内部自己同型の射影写像は
恒等写像のみである.よって直線体は可換である.
への射影写像で異なる.
これは単一性に反するので,直線体の内部自己同型の射影写像は
恒等写像のみである.よって直線体は可換である.
(2)![]() (3)
(2)が成り立つとする.
同一平面上の2直線
(3)
(2)が成り立つとする.
同一平面上の2直線![]() とその上の各3点
とその上の各3点![]() ,
,![]() がある.
3交点を
がある.
3交点を
![]() ,
,
![]() ,
,
![]() とおく.
直線
とおく.
直線![]() と
と
![]() の交点を
の交点を
![]() とする.射影写像
とする.射影写像
![]() を
を
逆に(3)が成り立つとする.
直線![]() 上の枠
上の枠
![]() を動かさない
任意の射影変換
を動かさない
任意の射影変換![]() をとる.点
をとる.点![]() を通る
を通る![]() と異なる直線
と異なる直線![]() をとり,
点
をとり,
点![]() を中心とする配景写像
を中心とする配景写像![]() を考える.
を考える.
![]() なので命題48によって
なので命題48によって
![]() となる点
となる点![]() が存在する.
が存在する.