 点を0次元射影空間とみるときは大文字で,射影空間の要素とみるときは小文字で表す.
点を0次元射影空間とみるときは大文字で,射影空間の要素とみるときは小文字で表す.
 点を0次元射影空間とみるときは大文字で,射影空間の要素とみるときは小文字で表す.
点を0次元射影空間とみるときは大文字で,射影空間の要素とみるときは小文字で表す.
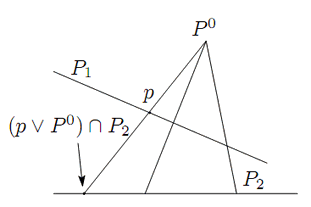
つまり,射影空間![]() の点
の点![]() に対して,
直線
に対して,
直線![]() と直線
と直線![]() の交点を対応させるのである.
の交点を対応させるのである.
これを一般化して射影空間![]() の部分空間から同一次元の部分空間への写像を定義する.そのために二つの命題を示す.
の部分空間から同一次元の部分空間への写像を定義する.そのために二つの命題を示す.
証明 次元定理から
証明
![\begin{eqnarray*}
&&[\{(x\vee {P_0}^{n-r-1})\cap{P_2}^r\}\vee {P_0}^{n-r-1}]\ca...
...e {P_0}^{n-r-1})\cap{P_1}^r
=x\vee({P_0}^{n-r-1}\cap{P_1}^r)=x
\end{eqnarray*}](images/img964.gif)
![]() の2点
の2点![]() をとる.この2点がそれぞれ
をとる.この2点がそれぞれ![]() と対応しているとする.
次元定理から
と対応しているとする.
次元定理から
![\begin{eqnarray*}
&&\dim[\{(x_1\vee x_2)\vee {P_0}^{n-r-1}\}\cap{P_2}^r]\\
&=...
...(x_1\vee x_2)\vee {P_0}^{n-r-1}\vee{P_2}^r\}\\
&=&n-r+1+r-n=1
\end{eqnarray*}](images/img971.gif)
証明
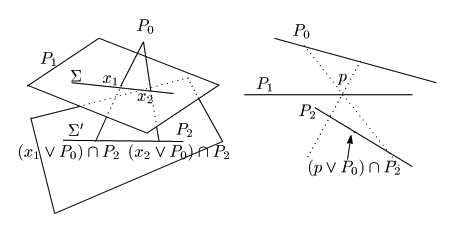
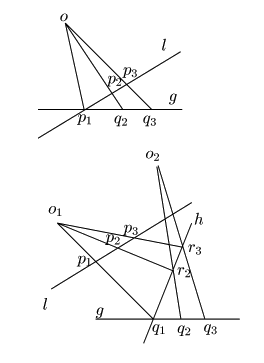 (1)
(1)
![]() で
で![]() のとき.
のとき.
公理II)によって,![]() と
と![]() は交わる.
交点を
は交わる.
交点を![]() とすれば,
とすれば,
![]() と
と
![]() は
は![]() を中心とする配景写像で対応する.つまり,
を中心とする配景写像で対応する.つまり,
![]() である.
である.
![]() のときも同様.
のときも同様.
(2)
![]() で
で
![]() のとき.
のとき.
2直線![]() と
と![]() で定まる平面上に,
で定まる平面上に,
![]() を通り
を通り![]() ,
,![]() と異なる直線
と異なる直線![]() を引く.
を引く.
![]() 上の点
上の点![]() をとり,
をとり,
![]() ,
,![]() と
と![]() の交点を
の交点を![]() とする.
(1)によって点
とする.
(1)によって点![]() で
で![]() を中心とする配景写像で
を中心とする配景写像で
![]() を
を
![]() に対応させるもの
に対応させるもの![]() が存在する.
この合成
が存在する.
この合成
![]() を
を![]() とすれば,
射影写像
とすれば,
射影写像![]() で
で
![]() と
と
![]() は対応する.
は対応する.
(3)
![]() のとき.
のとき.
![]() 上にない点
上にない点![]() と
と![]() と異なる直線
と異なる直線![]() をとる.
をとる.
![]() を中心とする
を中心とする![]() から
から![]() への配景写像で
への配景写像で
![]() と対応する点を
と対応する点を
![]() とする.
とする.
![]() と
と
![]() は射影写像で対応するので,この場合も成立する.
□
は射影写像で対応するので,この場合も成立する.
□
証明
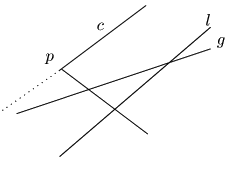 (1)
(1)
![]() のとき.
のとき.
![]() .この結果
.この結果
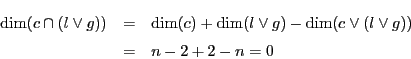
(2)
![]() のとき.
このとき
のとき.
このとき
![]() である.
したがって
である.
したがって
射影幾何の公理から展開するかぎり,![]() の1次元射影空間は,それだけではまったく身動きできない.公理II)が,直線がより次元の高い空間におかれていることが前提だからだ.
の1次元射影空間は,それだけではまったく身動きできない.公理II)が,直線がより次元の高い空間におかれていることが前提だからだ.![]() のとき,公理II)は自明な形で成立するだけである.1次元射影空間は,射影幾何の公理からそれ自身の内部で論を展開することはできない.
のとき,公理II)は自明な形で成立するだけである.1次元射影空間は,射影幾何の公理からそれ自身の内部で論を展開することはできない.
![]() のときはどのようになるか.2次元射影空間の内部では次のデザルグの定理が証明できない.つまりデザルグの定理は公理系からの帰結とはならない.2次元のなかだけで論を進めようとすれば,デザルグの定理を公理に加えなければならない.デザルグの定理を公理に加えることは,『射影幾何学』[35]の202頁にあるように,2次元射影空間が3次元空間のなかにおかれていると仮定するのと同値である.あるいは,『射影幾何学』[35]18頁にあるように,公理系を満たしデザルグの定理の成立しない2次元射影幾何を構成することもできる.
のときはどのようになるか.2次元射影空間の内部では次のデザルグの定理が証明できない.つまりデザルグの定理は公理系からの帰結とはならない.2次元のなかだけで論を進めようとすれば,デザルグの定理を公理に加えなければならない.デザルグの定理を公理に加えることは,『射影幾何学』[35]の202頁にあるように,2次元射影空間が3次元空間のなかにおかれていると仮定するのと同値である.あるいは,『射影幾何学』[35]18頁にあるように,公理系を満たしデザルグの定理の成立しない2次元射影幾何を構成することもできる.
次元が小さいと,このように特別なことが起こる.個別性を研究し,どこまでが一般的であって,どこからが次元に固有なことなのかを明らかにすることは重要なことではある.しかしわれわれは歴史的に3次元空間内で考えたことを,公理的に裏づけるという立場から進んできたので,今後,射影空間の次元![]() は
は![]() であるものとする.
であるものとする.
 (i)
(i)
証明
次元定理2と条件から
![]() について
について
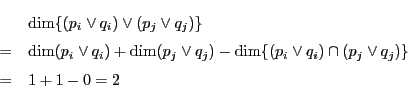
![\begin{eqnarray*}
d&=&\dim\{(p_1\vee q_1)\vee (p_2\vee q_2)\vee(p_3\vee q_3)\}\...
..._1\vee q_1)\vee (p_2\vee q_2)\}\cap (p_3\vee q_3)]\\
&=&3,\ 2
\end{eqnarray*}](images/img1037.gif)
これは平面
![]() 上に,
上に,![]() か
か![]() がないときである.
がないときである.
甲なら乙を示す.
乙なら甲を示す.
![]() について
について
![]() と
と![]() は交点をもつので,公理II)によって
は交点をもつので,公理II)によって
![]() と
と![]() も交点をもつ.
も交点をもつ.
![]() なので
なので
![]() .
これは
.
これは
![]() と
と![]() の交点と
の交点と
![]() と
と![]() の交点が一致し,その結果,
3直線が共点であることを示している.
の交点が一致し,その結果,
3直線が共点であることを示している.
![]() のとき.
のとき.
これは![]() も
も![]() も平面
も平面
![]() 上にあるときで,
2平面
上にあるときで,
2平面
![]() と
と
![]() が一致するときである.
が一致するときである.
甲なら乙を示す.
3直線
![]() が共有する点を
が共有する点を![]() とする.
平面
とする.
平面
![]() 上にない点
上にない点![]() をとる.
直線
をとる.
直線![]() 上の第3の点
上の第3の点![]() をとる.
をとる.![]() とし,
とし,
![]() に関して
公理II)を用いれば,
に関して
公理II)を用いれば,![]() と
と![]() は交点
は交点![]() をもつ.
をもつ.
![]() と
と
![]() に関してそれぞれ
に関してそれぞれ![]() の場合が適用できる.
各
の場合が適用できる.
各
![]() について,
について,
![]() と
と![]() の交点は
平面
の交点は
平面![]() と平面
と平面
![]() の上にあり,
の上にあり,
![]() と
と![]() の交点も
平面
の交点も
平面![]() と平面
と平面
![]() の上にある.
つまり
の上にある.
つまり![]() と
と![]() の交点であり一致する.
よって3点
の交点であり一致する.
よって3点
![]() は
は
![]() と
と
![]() の交わりの上にあり,共線である.
の交わりの上にあり,共線である.
乙なら甲を示す.
この場合すべて射影平面![]() の命題となる.
「乙なら甲」は「甲なら乙」の双対命題そのものなので成立する.
□
の命題となる.
「乙なら甲」は「甲なら乙」の双対命題そのものなので成立する.
□
今後,点を明記する必要があるときは「
![]() に関するデザルグの定理」ということにする.
に関するデザルグの定理」ということにする.
また![]() の場合は,
の場合は,![]() のなかで上記の点
のなかで上記の点![]() をとることができない.
だからこの証明は2次元射影空間
をとることができない.
だからこの証明は2次元射影空間![]() には適用できない.
には適用できない.
![]() において,ある命題の双対命題は,点と直線,記号
において,ある命題の双対命題は,点と直線,記号![]() と
と![]() をそれぞれ入れ替えたものである.
この方法によって上記命題の条件甲と条件乙が入れ替わる.
デザルグの定理の双対定理を作ると二つの同値な条件が入れ替わる.
したがって二つの条件の同値性を主張するデザルグの定理そのものである.
このように平面上の図形に関するデザルグの定理は自己双対である.
をそれぞれ入れ替えたものである.
この方法によって上記命題の条件甲と条件乙が入れ替わる.
デザルグの定理の双対定理を作ると二つの同値な条件が入れ替わる.
したがって二つの条件の同値性を主張するデザルグの定理そのものである.
このように平面上の図形に関するデザルグの定理は自己双対である.
命題36によって,
直線の配景写像,射影写像は,点を中心とするものを考えることによって,
一般的な考察ができる.以下,直線の配景写像,射影写像を考えるときは,
点を中心とするもので考える.
また,特にことわらないときは,
![]() 等は直線,
等は直線,![]() 等は点を表すものとする.
等は点を表すものとする.
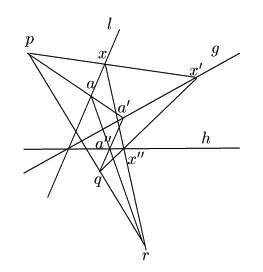 証明
証明
![]() に関するデザルグの定理から
3直線
に関するデザルグの定理から
3直線![]() ,
,![]() ,
,![]() は共点である.
この点を
は共点である.
この点を![]() とすれば,
とすれば,
![]() となる.
□
となる.
□
3直線![]() は共点でないとする.
は共点でないとする.
![]() と
と![]() ,
,![]() と
と![]() はそれぞれ同じ平面上にあり,交点をもつ.
それを
はそれぞれ同じ平面上にあり,交点をもつ.
それを
![]() とおく.
とおく.![]() は相異なり
は相異なり
![]() ,
,
![]() である.
点の配置によって場合分けして示す.
である.
点の配置によって場合分けして示す.
 (1)
(1)
![]() が一般の位置にあるとき.
つまり直線
が一般の位置にあるとき.
つまり直線![]() が点
が点![]() を通らないとき.
を通らないとき.
この場合命題38から,
![]() となる
となる![]() が存在する.
さらに逆写像
が存在する.
さらに逆写像
![]() をとる.
をとる.
![]() より
より
![]() である.
条件から
である.
条件から
![]() なので,直線
なので,直線![]() は点
は点![]() を通らない.
命題38から,
を通らない.
命題38から,
![]() となる
点
となる
点
![]() が存在する.
が存在する.
すなわち
![]() となる点
となる点![]() が存在した.
が存在した.
![]() が点
が点![]() を通らないときは
を通らないときは![]() に同様について,
同様の議論をすればよい.
に同様について,
同様の議論をすればよい.
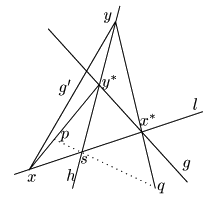 (2)
(2)
もし![]() なら
なら![]() も成り立つ.このとき
も成り立つ.このとき![]() となり自明である.
よって
となり自明である.
よって![]() とする.
とする.
(2-1)
![]() のとき.
のとき.![]() とする.
とする.
(2-1-1)
3点![]() が共線のとき.
が共線のとき.
(2-1-1-1)
![]() 上に
上に![]() と異なる点
と異なる点![]() が存在する場合.
命題38を用いて,直線
が存在する場合.
命題38を用いて,直線![]() を次の順序で直線
を次の順序で直線![]() にかえてゆけばよい.
にかえてゆけばよい.
(2-1-1-2)
![]() 上に
上に![]() と異なる点が存在しない場合.
この場合は
と異なる点が存在しない場合.
この場合は
![]() ,
,
![]() となる.
となる.
![]() とすると
とすると
![]() となり
となり![]() である.
である.
![]() はつねに成立するので
はつねに成立するので![]() は条件を満たす.
は条件を満たす.
(2-1-2)
3点![]() が共線でないとき.いいかえれば
が共線でないとき.いいかえれば
![]() かつ
かつ
![]() のとき.
(2-1-1-1)の
のとき.
(2-1-1-1)の![]() を
を![]() とすればよい.
とすればよい.
(2-2)
![]() のとき.
このときも
(2-1-1-1)の
のとき.
このときも
(2-1-1-1)の![]() を
を![]() とすればよい.
とすればよい.
以上ですべての場合が尽くされた.
□
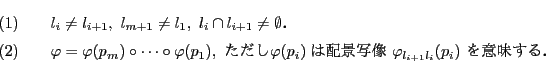
直線が3点のみからなる場合は, 命題36によって高々2つの配景写像の合成で表される. よって以下,直線は少なくとも4点を含むものとする.
![]() のとき,
のとき,![]() が高々2個の配景写像の合成になることを
が高々2個の配景写像の合成になることを
![]() に関する数学的帰納法で示す.
に関する数学的帰納法で示す.
![]() のときに示す.4直線を
のときに示す.4直線を
![]() と3点を
と3点を
![]() とする.
証明は4直線が一般の位置にない場合に示し,
一般の位置にあるときを逆に一般の位置にない場合に帰着させて示す.
とする.
証明は4直線が一般の位置にない場合に示し,
一般の位置にあるときを逆に一般の位置にない場合に帰着させて示す.
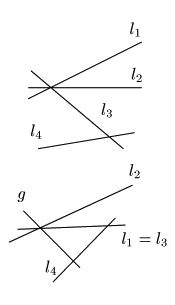 (1-1)
(1-1)
![]() が相異なり,かつ共点のとき.
命題37から
が相異なり,かつ共点のとき.
命題37から
![]() となる点
となる点![]() が存在し,
が存在し,
![]() となる.
となる.
![]() が相異なり,かつ共点のときも同様である.
が相異なり,かつ共点のときも同様である.
(1-2)
![]() で
で![]() との交点
との交点![]() が
が![]() 上にないとき.
上にないとき.
![]() と
と![]() の交点を
の交点を![]() とする.
とする.
![]() ,
,![]() ,
,![]() のいずれとも異なる
のいずれとも異なる![]() 上の点が存在するので,それを
上の点が存在するので,それを![]() とする.
とする.![]() とする.命題38によって,写像
とする.命題38によって,写像
![]() の
の![]() を
を![]() で置きかえることができる.
この結果
で置きかえることができる.
この結果![]() が共点の場合に帰着できる.
が共点の場合に帰着できる.
![]() で
で![]() との交点
との交点![]() が
が![]() 上にないときも同様である.
上にないときも同様である.
 (1-3)
(1-3)
![]() ,
,![]() のとき.
この2直線の交点を
のとき.
この2直線の交点を![]() とし,
とし,![]() を通る直線
を通る直線![]() をとる.
同じ平面上の点
をとる.
同じ平面上の点![]() を中心とする配景写像
を中心とする配景写像
![]() をとり,射影変換
をとり,射影変換
![]() ,
つまり
,
つまり
![]() を考える.命題37により,
を考える.命題37により,
![]() を
を![]() におきかえることができる.順次これを行うことで
におきかえることができる.順次これを行うことで
![]() と表すことができる.よって
と表すことができる.よって
![]() である.
である.
(1-4)
![]() が相異なり,かつ共点のとき.
が相異なり,かつ共点のとき.
![]() を
を
![]() に置きかえることができる.
に置きかえることができる.
![]() は一つに置き換わるので,この場合も成立する.
は一つに置き換わるので,この場合も成立する.
![]() が相異なり,かつ共点のときも同様.
が相異なり,かつ共点のときも同様.
(2)
3直線で共点であるものがない場合.
4直線はすべて異なる.
![]() と
と![]() の交点を
の交点を![]() とする.
とする.
![]() 上になく
上になく![]() でもない
でもない![]() 上の点をとり
上の点をとり![]() とする.
とする.
![]() とし,
とし,![]() を
を![]() に置きかえる.これで
に置きかえる.これで![]() が共点となり,
(1-1)に帰着する.
が共点となり,
(1-1)に帰着する.
以上で![]() の場合は成立した.
の場合は成立した.
(3)
![]() とし
とし![]() までは成立するとする.
までは成立するとする.
![]() の
の![]() で
で
![]() となるところがあれば,
となるところがあれば,
![]() に以上の操作を行い配景写像をひとつ減らすことができる.
に以上の操作を行い配景写像をひとつ減らすことができる.
![]() について
について![]() なら,
なら,
![]() はすべて異なる.
よって命題39によって
はすべて異なる.
よって命題39によって![]() を別の直線
を別の直線![]() に置きかえることができる.
この場合
に置きかえることができる.
この場合![]() なので,
なので,
![]() でひとつ減らすことができる.
帰納法の仮定からこの場合も成立する.
□
でひとつ減らすことができる.
帰納法の仮定からこの場合も成立する.
□