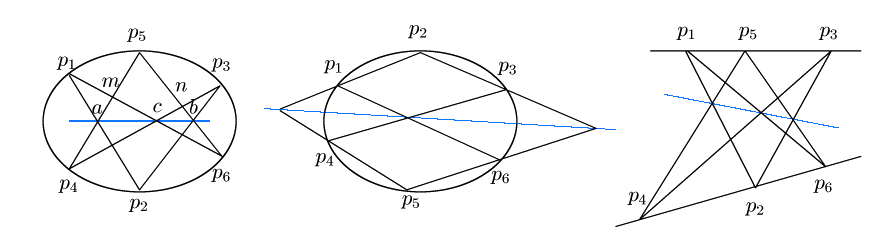
が共線であることである. ■
この事実をすでにパスカルは認識していた. そしてパスカルの定理を二つの円の場合に証明すれば, これによって任意の二つの円錐曲線で成立することを知っていた.
二つの円の場合の証明は,先に「円周角の相等を用いる」でおこなった方法であったと言われている.二つの円の場合は,これをユークリッド平面に置くことができ,そこでは長さの相等や円周角の定理が使える.これを用いて証明した.
「パスカルの定理は射影幾何の定理」にはもう一つの意味がある. つまりその証明もまた射影幾何内部の方法で完結してできるはずだということである.
そのためには射影幾何の公理系から再出発し,必要なことをすべてを再構成しなければならない. われわれはそれを準備してきた.その結果, パスカルの定理を射影幾何の内部で証明することができるようになっている.
パスカルの定理を再掲し, その証明を射影幾何内部の方法で行おう.
これは点がどの順に並んでいてもよい.
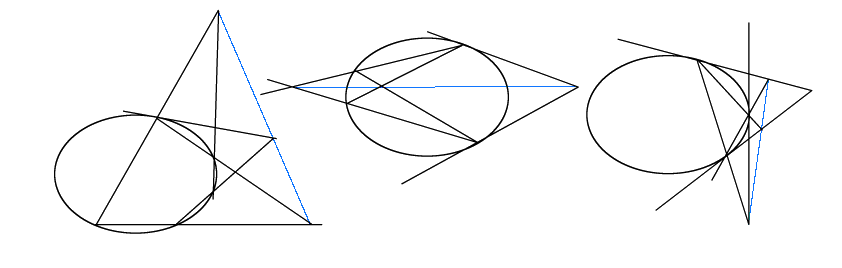
また![]() が正則でなく2直線に分解していてもよい.
証明は正則な場合で考えるが,
それが分解しているときにもそのまま適用されることを追認できる.
が正則でなく2直線に分解していてもよい.
証明は正則な場合で考えるが,
それが分解しているときにもそのまま適用されることを追認できる.