

 次: 座標三角形による証明
上: パスカルの定理
前: 射影幾何の定理
次: 座標三角形による証明
上: パスカルの定理
前: 射影幾何の定理
平面におかれた二次曲線の
二つの定義の同等性はすでに示されているので,
証明の方法によって適切な定義を選べばよい.
二次曲線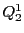 の定義として定義30を用い,
この定義のもと,複比で表された射影幾何の基本性質からパスカルの定理が次のように示される.
の定義として定義30を用い,
この定義のもと,複比で表された射影幾何の基本性質からパスカルの定理が次のように示される.
とおく.また
とする.複比の相等
が成り立つ.この結果,命題67によって
3直線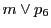 ,
,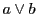 ,
,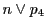 は共点である.
つまり
は共点である.
つまり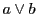 上に
上に
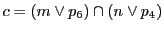 があり,
3点
があり,
3点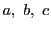 は共線である.
は共線である.
逆に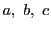 が共線であるとする.このとき
が共線であるとする.このとき
線束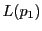 の3直線
の3直線
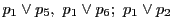 を
線束
を
線束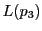 の3直線
の3直線
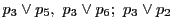 に
うつす射影写像をとると,
線束の複比の定義と命題64によって,この射影写像で
に
うつす射影写像をとると,
線束の複比の定義と命題64によって,この射影写像で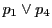 も
も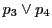 にうつる.
よってこの線束間の射影写像で定まる
にうつる.
よってこの線束間の射影写像で定まる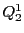 の上に
6点
の上に
6点
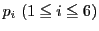 が存在する.
□
が存在する.
□
この証明は複比で記述したが,二次曲線の射影写像による定義を,配景写像,射影写像の基本性質と結びつけたものである.
2014-01-03
![\begin{eqnarray*}
% latex2html id marker 35519
&&[p_5,\ m;\ a,\ p_4]\\
(命?...
...vee p_6;\ p_3\vee p_2,\ p_3\vee p_4]\\
&=&[p_5,\ p_6;\ b,\ n]
\end{eqnarray*}](images/img2385.gif)
![]() が共線であるとする.このとき
が共線であるとする.このとき
![\begin{eqnarray*}
&&[p_1\vee p_5,\ p_1\vee p_6;\ p_1\vee p_2,\ p_1\vee p_4]\\
...
...\\
&=&[p_3\vee p_5,\ p_3\vee p_6;\ p_3\vee p_2,\ p_3\vee p_4]
\end{eqnarray*}](images/img2389.gif)
![]() の3直線
の3直線
![]() を
線束
を
線束![]() の3直線
の3直線
![]() に
うつす射影写像をとると,
線束の複比の定義と命題64によって,この射影写像で
に
うつす射影写像をとると,
線束の複比の定義と命題64によって,この射影写像で![]() も
も![]() にうつる.
よってこの線束間の射影写像で定まる
にうつる.
よってこの線束間の射影写像で定まる![]() の上に
6点
の上に
6点
![]() が存在する.
□
が存在する.
□