- (i)
- 一つの正則な二次曲線
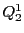 に接している.
に接している.
- (ii)
- 2つの線束に属する.
が共点であることである. ■
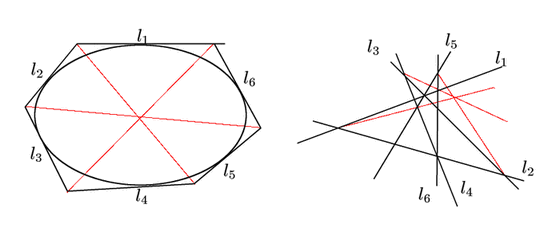
二次曲線![]() が正則な場合のこの双対命題を
ブリアンションの定理という.
ブリアンションは1806年,二次曲線
が正則な場合のこの双対命題を
ブリアンションの定理という.
ブリアンションは1806年,二次曲線![]() が正則な場合にパスカルの定理の双対命題としてこれを得た.
パスカルの定理から150年後のことであった.
が正則な場合にパスカルの定理の双対命題としてこれを得た.
パスカルの定理から150年後のことであった.
直線上に異なる3点
をとり, と 直線
上に異なる3点
をとる.
直線と直線
の交点を
, 直線
と直線
の交点を
, 直線
と直線
の交点を
とする.
このとき3点は一直線上にある. ■
2直線の方程式の積から作られる方程式を![]() とし,
二次曲線
とし,
二次曲線![]() を考えることで,
複比による証明と代数的な証明がそのまま適用される.
を考えることで,
複比による証明と代数的な証明がそのまま適用される.