1828年にC.G.J.ヤコビ(1804〜1851)はクレレ誌に楕円関数を使った閉形定理の証明を発表した. 彼は実平面上の二円,一方は他方の円の内部にある場合に閉形定理を証明した. 射影することによって,定理は一方が他方の内部にある二つの楕円の場合に一般化できることをヤコビは注意している.
実際, また,「円に還元する別証明」5.1.2で述べたように,実平面上での射影幾何の命題の証明は, 複素射影空間での命題の証明となる.
また『数学点描』[35]で著者のシェーンベルグは,
ベルトラン(J.Bertrand)がヤコビ(Jacobi)のものとする方法で証明する.しかし,ヤコビの著作集の第1巻にある回顧録を調べてみると,この証明はヤコビよりもむしろベルトランによるものだということがわかる.これは初等微分積分学の幾何学へのひとつの注目すべき応用である.と述べ,解析的なポンスレの定理の証明を行っている. これとまったく同じ内容が,高校生向けに書かれた『高校生に贈る数学II』[36]の中で, 「ヤコビの証明の考え方に基づく,もう少し簡単化されたベルトランの証明を述べてみます」との前置きのもとに書かれている. ここでそれを再構成しよう.
実平面におかれた二円![]() と
と![]() がある.
同心円ならポンスレの定理は自明なので,
同心ではないとし,
それぞれの中心は
がある.
同心円ならポンスレの定理は自明なので,
同心ではないとし,
それぞれの中心は
![]() ,半径は
,半径は![]() で,
円
で,
円![]() は円
は円![]() の内部にあり,2円の中心間の距離は
の内部にあり,2円の中心間の距離は![]() であるとする.
直線
であるとする.
直線![]() と
と![]() の交点のうち,
の交点のうち,![]() との距離が大きいものを
との距離が大きいものを![]() とする.
とする.
![]() 上の点
上の点![]() に対して
に対して![]() から
から![]() への左回りの角を
への左回りの角を![]() とおく.
この角に対する点であることを明示するときは
とおく.
この角に対する点であることを明示するときは
![]() と書く.
と書く.
![]() 上の点
上の点![]() をとる.
点
をとる.
点![]() を点
を点![]() の位置から左回りに円
の位置から左回りに円![]() 上を動かし,
弦
上を動かし,
弦![]() が最初に円
が最初に円![]() と接するとき,
その位置の
と接するとき,
その位置の![]() あらためて
あらためて![]() とする.
また接点を
とする.
また接点を![]() とする.
点
とする.
点![]() は点
は点![]() に対して一意に定まり,
に対して一意に定まり,
![]() から
から![]() への左回りの角を
への左回りの角を![]() とすると,
とすると,
![]() は
は![]() の関数である.これを明示するときは
の関数である.これを明示するときは
![]() と書く.また
と書く.また
![]() とも書ける.
とも書ける.
三平方の定理と余弦定理から
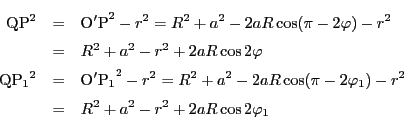
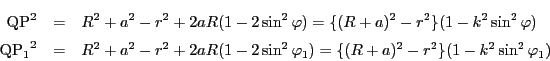
 命題 101
命題 101
![]() の関数
の関数
![]() の導関数について
の導関数について
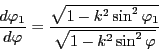
証明
微少な角
![]() をとり,
をとり,
![]() とおく.
また
とおく.
また
![]() とし,
とし,
![]() ,
,
![]() とする.
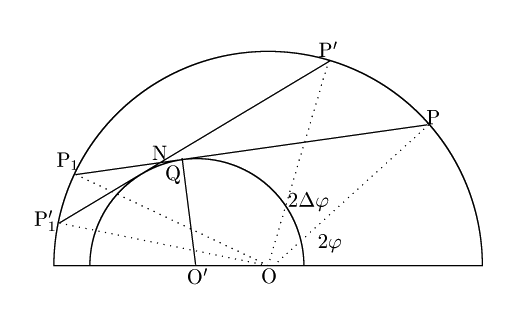
2弦
とする.
2弦![]() と
と
![]() の交点を
の交点を![]() とする.
とする.
![]() と
と
![]() の相似と,
弦の長さに円弧の長さが比例することより
の相似と,
弦の長さに円弧の長さが比例することより
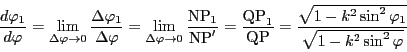
上記証明は簡明であるが,微少な角における円弧と弦の比の相等を用いている. それによらず,直接に示すことができる.
別証明
図形を,![]() を原点に,
を原点に,![]() を
を![]() 軸として座標平面に置く.
軸として座標平面に置く.
![]() 上の2点
上の2点
![]() と
と
![]() の座標は
の座標は
![]() ,
,
![]() であるから,
直線
であるから,
直線![]() の方程式は
の方程式は
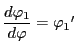 とおく.
とおく.
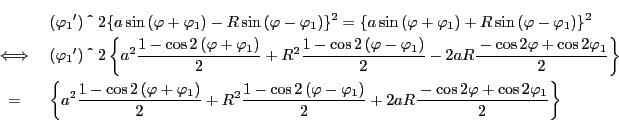
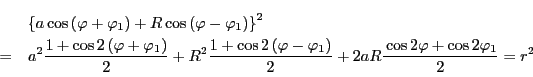
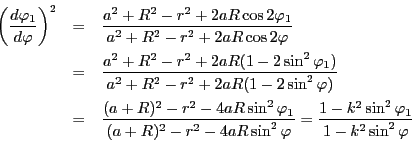
命題101の別証明が得られた. □
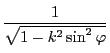 の定積分について
の定積分について
証明
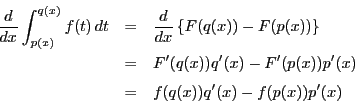
証明 補題21より
この命題を用いて円の場合にポンスレの定理を証明する. 補題が必要である.
証明
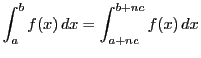 なので
なので
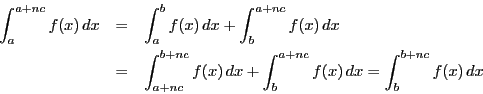
![]() は,
は,
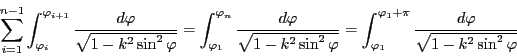
一方,命題102より
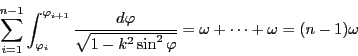
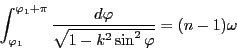
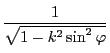 は周期
は周期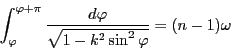
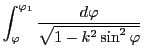 は楕円の弧長の計算過程で現れる積分なので楕円積分といわれる.証明の基本は,2つの円の一方に接する直線が他方と交わるときの2つの交点の位置関係に関する不変量が楕円積分を用いることで得られるという命題102である.この命題の下でポンスレの定理そのものは周期関数の定積分のもつ性質として示される.
は楕円の弧長の計算過程で現れる積分なので楕円積分といわれる.証明の基本は,2つの円の一方に接する直線が他方と交わるときの2つの交点の位置関係に関する不変量が楕円積分を用いることで得られるという命題102である.この命題の下でポンスレの定理そのものは周期関数の定積分のもつ性質として示される.