

 次: 楕円関数による証明
上: 代数幾何へ
前: 代数幾何へ
次: 楕円関数による証明
上: 代数幾何へ
前: 代数幾何へ
本節以降は研究ノートである.
証明が出来ていないことも述べつつ,順次書いてゆく.
したがってそのつど必要な改訂がなされる.
この節はこれまで展開してきたことをこえる内容を前提とする.
つまり,楕円積分と楕円関数の解析理論の基礎と,
楕円曲線の代数幾何的理論である.
この分野の基本事項については,必要なことを証明なしに明示しつつ,進みたい.
したがって,この節以下は自己完結ではない.
ヤコビの証明では,
2つの円の一方に接する直線が他方と交わるときの2つの交点の位置関係に関する不変量が,
楕円積分を用いることで得られるという命題102を示した.
これがポンスレの定理の根拠であった.
この基本思想のもと,ケーリーはさらに考察を深めた.
ケーリー(Arthur Cayley)の論文集第2巻[42]所収の第113論文である.
このケーリーの方法をもとに,
ポンスレの定理12の楕円関数による証明を再構成する.
ケーリーはさらに,
ポンスレの閉形定理が成立するための2つの円錐曲線に関する条件を導きその結論を述べた.
それが論文集第2巻[42]所収の第115,116論文である.
しかしそこに証明はない.
ところが1978年に,Griffiths と Harrisによって代数幾何的な証明がなされる.
それが『ON CAYLEY'S EXPLICIT SOLUTION TO PONCELET'S PORISM』[39]である.
さらにこれは『Poncelet's Theorem』[40]で包括的に展開されている.
また,『Poncelet Porisms and Beyond』[41]ではさらに高次の場合にも拡張して,今日の問題まで述べられている.
2012年7月に,これらをご教示いただいた有本彰雄先生に心から感謝する.
この理論は本質的にリーマン面の解析的な理論にもとづいている.まずこの内容を再構成し,第116論文の定理を証明することをめざす.
ポンスレの定理そのものは,楕円曲線の代数的方法で証明される.
それが『代数幾何学』[38]においてなされている.
この本の13章の冒頭「前章でポンスレの定理の証明が完成したが,
この定理は『いつ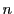 角形が描けるのか』については何もいっていない.
この問題を考えていくのがこの章の目標である」と書かれているが,
ポンスレ多角形のケーリーによる条件までは至っていない.
ケーリーによる条件はどこまで代数的理論の範囲で求まるのか.
あるいは解析理論なしには不可能なのか,ここを見極めたい.
角形が描けるのか』については何もいっていない.
この問題を考えていくのがこの章の目標である」と書かれているが,
ポンスレ多角形のケーリーによる条件までは至っていない.
ケーリーによる条件はどこまで代数的理論の範囲で求まるのか.
あるいは解析理論なしには不可能なのか,ここを見極めたい.
以上のような目標をたて勉強をはじめたのが,2012年の5月であった.
以下はその過程をそのままにおく.
行列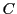 で定まる円錐曲線
で定まる円錐曲線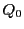 と行列
と行列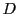 で定まる円錐曲線
で定まる円錐曲線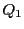 がある.
これらの円錐曲線は一般の位置にあるとする.
つまり異なる4点を共有しているとする.
以下において,言割らずともそうであるとする.
がある.
これらの円錐曲線は一般の位置にあるとする.
つまり異なる4点を共有しているとする.
以下において,言割らずともそうであるとする.
一般の位置にない場合のポンスレの定理は,すでに一つの問題が未解決のままおかれている.一方で,『Poncelet's Theorem』[40]では一般の位置にない場合についても包括的に述べている.
この分野の研究は,一般の位置にある場合の課題に目処をつけて後,時間が許せば取りかかりたい.
2014-01-03