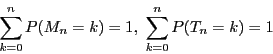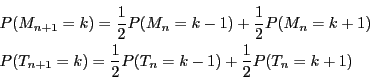��: �A���Ȋm��
��: �����W�{���
�O: �����̊m��1
��: �A���Ȋm��
��: �����W�{���
�O: �����̊m��1
�����̊m��2
���̓��������l���Ă݂悤�D
��
(1)
1��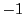 �̒l���Ƃ�m���ϐ�
�̒l���Ƃ�m���ϐ�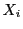 �́C
�́C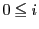 �ɑ��A
�ɑ��A
�ł���Ƃ���D���̂Ƃ�
�ł���D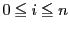 �ɑ��C
�ɑ��C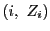 �����W���ʏ�ɂƂ�D
�����W���ʏ�ɂƂ�D
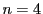 �̂Ƃ��D
���s�̑�����
�̂Ƃ��D
���s�̑�����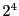 �ł���D
��������ƂɁC��������
�ł���D
��������ƂɁC��������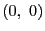 ����̌o�H�̑����𐔂��邱�Ƃɂ��C���̌��ʂ�D
����̌o�H�̑����𐔂��邱�Ƃɂ��C���̌��ʂ�D
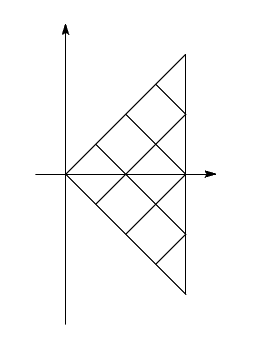
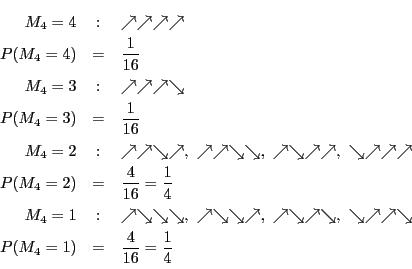
�����āC
���C
(2)
���l�ɍl����D
�����āC
���C
(3)
(2)�Ɠ��l�ɁC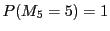 �C
�C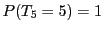 �ł���D
�܂��C
�ł���D
�܂��C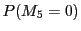 ��
��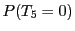 �����̎��ۂ̘a�̗]���ۂł��邱�Ƃ����l�ł���D
�����̎��ۂ̘a�̗]���ۂł��邱�Ƃ����l�ł���D
�����ŁC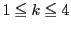 �ɑ��āC
�ɑ��āC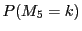 ��
��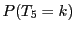 ��
���ꂼ��C
��
���ꂼ��C
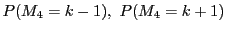 ��
��
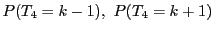 �ŕ\���D
�ŕ\���D
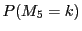 �ɂ��āD
�ɂ��āD
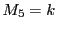 �ƂȂ鎖�ۂ́C
�ƂȂ鎖�ۂ́C
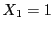 �Ȃ�C��������͂��߂Ďc��4��̎��s��
�Ȃ�C��������͂��߂Ďc��4��̎��s��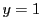 ����̐������̍ő�Έʂ�
����̐������̍ő�Έʂ�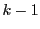 �ƂȂ�C
�ƂȂ�C
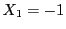 �Ȃ�C��������͂��߂Ďc��4��̎��s��
�Ȃ�C��������͂��߂Ďc��4��̎��s��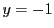 ����̐������̍ő�Έʂ�
����̐������̍ő�Έʂ�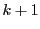 �ƂȂ�悤�Ȏ��ۂł���D
�ƂȂ�悤�Ȏ��ۂł���D
����āC
�����藧�D
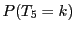 �ɂ��āD
�ɂ��āD
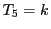 �ƂȂ鎖�ۂ́C
�ƂȂ鎖�ۂ́C
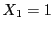 �̂Ƃ��D2��ڂ���͂��߂Ďc��4��̎��s�ŁC
�̂Ƃ��D2��ڂ���͂��߂Ďc��4��̎��s�ŁC
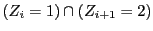 ��
��
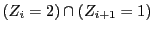 ��
��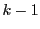 ��N����Ƃ���D
���̂Ƃ��C����
��N����Ƃ���D
���̂Ƃ��C����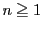 �̕����ł�
�̕����ł�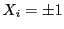 ��
��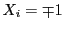 �ɒu�������ē����鎎�s���l����ƁC
1��ڂ̎��s�Ƃ��킹��
�ɒu�������ē����鎎�s���l����ƁC
1��ڂ̎��s�Ƃ��킹��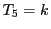 �ƂȂ鎖�ۂ�������D
�ƂȂ鎖�ۂ�������D
�t�ɁC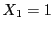 ��
��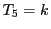 �ƂȂ鎖�ۂ���t�̒u�������ŁC
�ƂȂ鎖�ۂ���t�̒u�������ŁC
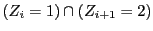 ��
��
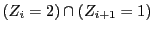 ��
��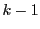 ��N���鎖�ۂ�������D
��N���鎖�ۂ�������D

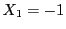 �Ȃ�C2��ڂ���͂��߂Ďc��4��̎��s�ŁC
�Ȃ�C2��ڂ���͂��߂Ďc��4��̎��s�ŁC
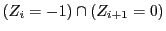 ��
��
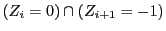 ��
��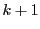 ��N����Ƃ���D
�ŏ���
��N����Ƃ���D
�ŏ���
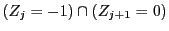 �ƂȂ�
�ƂȂ�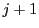 �ɑ��C
�ɑ��C
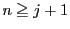 �̕����ł�
�̕����ł�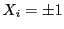 ��
��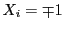 �ɒu�������ē����鎎�s���l����ƁC
����ɂ����
�ɒu�������ē����鎎�s���l����ƁC
����ɂ����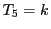 �ƂȂ鎖�ۂ���������D
�ƂȂ鎖�ۂ���������D
�t�ɁC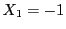 ��
��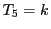 �ƂȂ鎖�ۂ���t�̒u�������ŁC
�ƂȂ鎖�ۂ���t�̒u�������ŁC
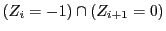 ��
��
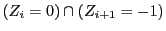 ��
��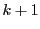 ��N���鎖�ۂ�������D
��N���鎖�ۂ�������D

���������āC
�����藧�D
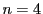 �̂Ƃ���
�̂Ƃ���
�ł������̂ŁC���̑Q������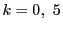 �̂Ƃ��̍l�@����
�̂Ƃ��̍l�@����
���C�ӂ�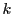 �ɑ��Đ��藧�D
�ɑ��Đ��藧�D
�������ʉ����Ă݂悤�D
�ȉ��C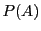 �Ŏ���
�Ŏ���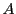 �̊m����\���C
�̊m����\���C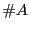 �͏W��
�͏W��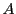 �̗v�f�̌���\�����̂Ƃ���D
�̗v�f�̌���\�����̂Ƃ���D
��� 2
1��
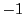
�̒l���Ƃ�m���ϐ�
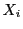
���C
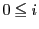
�ɑ��A
�Œ�߂�D�����āC
�Ƃ����D
-
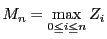 �Ƃ���Ƃ��C
�m��
�Ƃ���Ƃ��C
�m��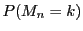 ��
��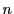 ��
��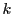 ��p���ĕ\���D
��p���ĕ\���D
-
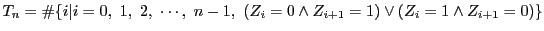 �Ƃ���.
���̂Ƃ��C�C�ӂ̎��R��
�Ƃ���.
���̂Ƃ��C�C�ӂ̎��R��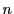 ��
��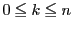 �ɑ���
�ɑ���
�����藧���Ƃ������D
��
(1)
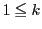 ���Œ肵�C
���Œ肵�C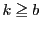 �ƂȂ�
�ƂȂ�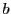 ���Ƃ�D
���Ƃ�D
�����藧�D
�Ȃ��Ȃ�C
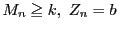 �ƂȂ��̎��ۂɑ��āC
�ŏ���
�ƂȂ��̎��ۂɑ��āC
�ŏ���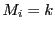 �ƂȂ�
�ƂȂ�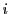 ���߁C
���߁C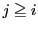 �͈̔͂�
�͈̔͂�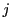 �ɑ�
�ɑ�
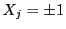 �Ȃ�C�����
�Ȃ�C�����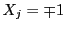 �ɂ������������ۂ��Ƃ�ƁC
����́C
�ɂ������������ۂ��Ƃ�ƁC
����́C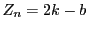 �����D
�����D
�t�ɁC
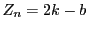 �ƂȂ��̎��ۂɑ��āC
�ƂȂ��̎��ۂɑ��āC
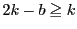 ���ŏ���
���ŏ���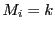 �ƂȂ�
�ƂȂ�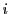 ������D
������D
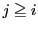 �͈̔͂�
�͈̔͂�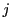 �ɑ�
�ɑ�
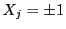 �Ȃ�C�����
�Ȃ�C�����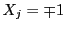 �ɂ������������ۂ��Ƃ�ƁC
����́C
�ɂ������������ۂ��Ƃ�ƁC
����́C
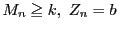 �����D
�����D
���̑Ή��͈�Έ�ł���̂�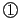 �����藧�D
���������āC
�����藧�D
���������āC
�ł���D����āC
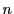 �C
�C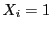 �ƂȂ�
�ƂȂ�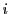 ��
��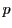 �C
�C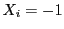 �ƂȂ�
�ƂȂ�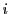 ��
��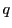 �Ƃ���D
�Ƃ���D
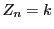 �Ƃ������Ƃ�
�Ƃ������Ƃ�
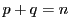 ����
����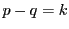 �Ȃ̂ŁC
�Ȃ̂ŁC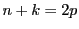 �ł���D����������
�ł���D����������
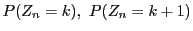 �̈����0�ł���D
�̈����0�ł���D
���������āC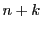 �������̂Ƃ��D
�������̂Ƃ��D
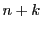 ����̂Ƃ��D
����̂Ƃ��D
�ł���D������܂Ƃ߂āC
�ƕ\�����Ƃ��ł���D������![$[x]$](images/img99.gif) ��
��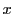 ���Ȃ��ő�̐�����\���D
���Ȃ��ő�̐�����\���D
(2)
���ׂĂ�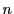 �ɑ��āC
�ɑ��āC
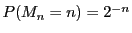 �C
�C
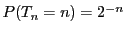 �Ȃ̂ŁC
�Ȃ̂ŁC
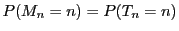 �ł���D
�ł���D
�܂��C
�ł���D
���ꂩ��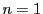 �̂Ƃ���ӂ͐�������D
�̂Ƃ���ӂ͐�������D
���R��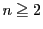 �ɑ��āC
�ɑ��āC
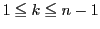 �̂Ƃ��C
�̂Ƃ��C
�����藧���Ƃ������C
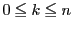 �̂Ƃ���������D
�̂Ƃ���������D
���R��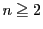 �ɑ��āC
�ɑ��āC
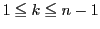 �̂Ƃ��C
�̂Ƃ��C
�����藧���Ƃ𐔊w�I�A�[�@�Ŏ����D
�����ŁC
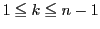 �ɑ��āC
�ɑ��āC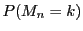 ��
��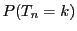 ��
���ꂼ��C
��
���ꂼ��C
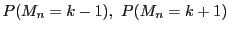 ��
��
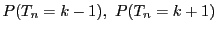 �ŕ\���D
�ŕ\���D
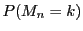 �ɂ��āC
�ɂ��āC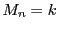 �ƂȂ鎖�ۂ́C
�ƂȂ鎖�ۂ́C
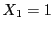 �Ȃ�C��������͂��߂Ďc��
�Ȃ�C��������͂��߂Ďc��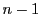 ��̎��s��
��̎��s��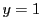 ����̐������̍ő�Έʂ�
����̐������̍ő�Έʂ�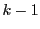 �ƂȂ�C
�ƂȂ�C
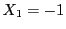 �Ȃ�C��������͂��߂Ďc��
�Ȃ�C��������͂��߂Ďc��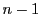 ��̎��s��
��̎��s��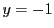 ����̐������̍ő�Έʂ�
����̐������̍ő�Έʂ�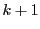 �ƂȂ�悤�Ȏ��ۂł���D
�ƂȂ�悤�Ȏ��ۂł���D
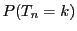 �ɂ��āC
�ɂ��āC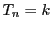 �ƂȂ鎖�ۂ́C
�ƂȂ鎖�ۂ́C
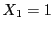 �̂Ƃ��D2��ڂ���͂��߂Ďc��
�̂Ƃ��D2��ڂ���͂��߂Ďc��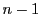 ��̎��s�ŁC
��̎��s�ŁC
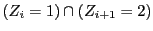 ��
��
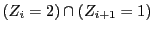 ��
��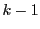 ��N����Ƃ���D
���̂Ƃ��C����
��N����Ƃ���D
���̂Ƃ��C����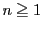 �̕����ł�
�̕����ł�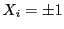 ��
��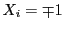 �ɒu�������ē����鎎�s���l����ƁC
1��ڂ̎��s�Ƃ��킹��
�ɒu�������ē����鎎�s���l����ƁC
1��ڂ̎��s�Ƃ��킹��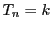 �ƂȂ鎖�ۂ�������D
�ƂȂ鎖�ۂ�������D
�t�ɁC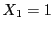 ��
��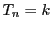 �ƂȂ鎖�ۂ���t�̒u�������ŁC
�ƂȂ鎖�ۂ���t�̒u�������ŁC
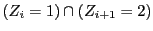 ��
��
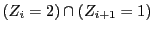 ��
��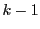 ��N���鎖�ۂ�������D
��N���鎖�ۂ�������D
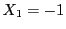 �Ȃ�C2��ڂ���͂��߂Ďc��
�Ȃ�C2��ڂ���͂��߂Ďc��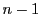 ��̎��s�ŁC
��̎��s�ŁC
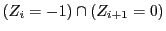 ��
��
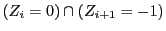 ��
��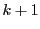 ��N����Ƃ���D
�ŏ���
��N����Ƃ���D
�ŏ���
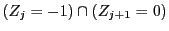 �ƂȂ�
�ƂȂ�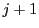 �ɑ��C
�ɑ��C
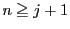 �̕����ł�
�̕����ł�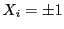 ��
��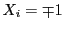 �ɒu�������ē����鎎�s���l����ƁC
����ɂ����
�ɒu�������ē����鎎�s���l����ƁC
����ɂ����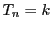 �ƂȂ鎖�ۂ�1������D
�ƂȂ鎖�ۂ�1������D
�t�ɁC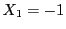 ��
��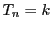 �ƂȂ鎖�ۂ���t�̒u�������ŁC
�ƂȂ鎖�ۂ���t�̒u�������ŁC
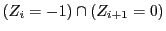 ��
��
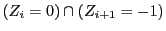 ��
��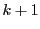 ��N���鎖�ۂ�������D
��N���鎖�ۂ�������D
�ォ��C�Q����
�����藧�D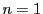 �̂Ƃ��̐�������C
�̂Ƃ��̐�������C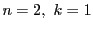 ���������C
���������C
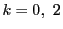 �̂Ƃ��̍l�@�Ƃ��킹�āC
�̂Ƃ��̍l�@�Ƃ��킹�āC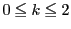 �ɑ���
��������D
�ɑ���
��������D
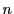 �̂Ƃ��C
�̂Ƃ��C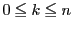 �ɑ��Đ�������Ƃ���ƁC�Q�������������̂ŁC
�ɑ��Đ�������Ƃ���ƁC�Q�������������̂ŁC
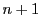 �̂Ƃ��C
�̂Ƃ��C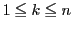 �ɂ��Đ������C
�ɂ��Đ������C
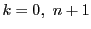 �̂Ƃ��̍l�@�Ƃ��킹�āC
�̂Ƃ��̍l�@�Ƃ��킹�āC
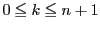 �ɂ��Đ�������D
�ɂ��Đ�������D
����āC
�����藧���Ƃ������ꂽ�D


 ��: �A���Ȋm��
��: �����W�{���
�O: �����̊m��1
Aozora�@
2017-10-22
��: �A���Ȋm��
��: �����W�{���
�O: �����̊m��1
Aozora�@
2017-10-22
![]() ��J��Ԃ����ۂ̑��v�z�̍��v��
��J��Ԃ����ۂ̑��v�z�̍��v��![]() (���~)�Ƃ���D�������C
(���~)�Ƃ���D�������C![]() �Ƃ���D
�Ƃ���D
![]() �Ƃ���Ƃ��C�m��
�Ƃ���Ƃ��C�m��![]() �C
�C
![]() �̒l�����ꂼ�ꋁ�߂�D�������C
�̒l�����ꂼ�ꋁ�߂�D�������C
![]() ��
��![]() �ɂ�����
�ɂ�����![]() �̍ő�l��\���D
�̍ő�l��\���D
![]() �Ƃ���Ƃ��C�m��
�Ƃ���Ƃ��C�m��![]() �C
�C
![]() �̒l�����ꂼ�ꋁ�߂�D�������C
�̒l�����ꂼ�ꋁ�߂�D�������C![]() �͏W��
�͏W��![]() �̗v�f�̌���\���D
�̗v�f�̌���\���D
![]() �ɑ���
�ɑ���![]() ��
��![]() �̊Ԃɐ��藧�W�����߂�D
�̊Ԃɐ��藧�W�����߂�D

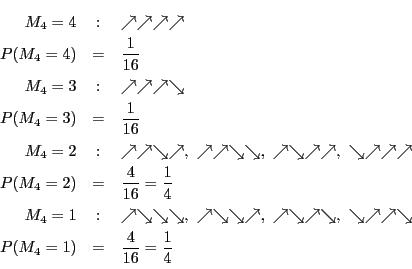
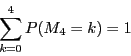
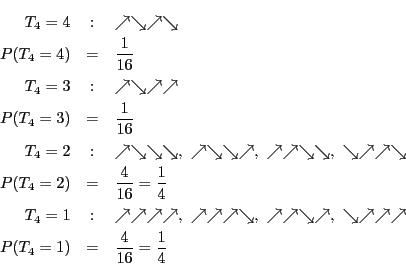
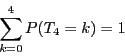


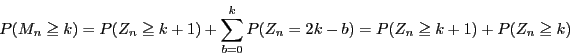
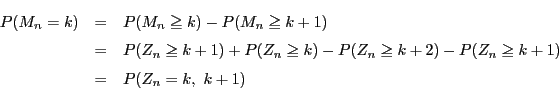
![\begin{displaymath}
P(M_n=k)={}_n \mathrm{C}_{\left[\dfrac{n+k+1}{2}\right]}\cdot 2^{-n}
\end{displaymath}](images/img98.gif)