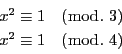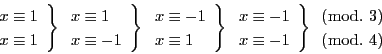次: オイラーの関数
上: 合同式
前: 一次合同方程式
次: オイラーの関数
上: 合同式
前: 一次合同方程式
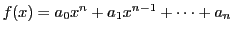 が整数係数の多項式であるとき,合同方程式
が整数係数の多項式であるとき,合同方程式
を満たす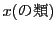 を求めることを考える.このときは,各係数
を求めることを考える.このときは,各係数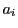 をそれと合同な数で
置き換えてもかまわない.特に
をそれと合同な数で
置き換えてもかまわない.特に で割りきれる係数は消し去ってかまわない.このような消
去をおこなった後に
で割りきれる係数は消し去ってかまわない.このような消
去をおこなった後に
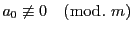 なら,この合同方程式を
なら,この合同方程式を 次という.
合同方程式の解法に関する三つの基本定理を証明しよう.
次という.
合同方程式の解法に関する三つの基本定理を証明しよう.
定理 14
法

が素数であるとき,

次の合同方程式
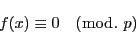 |
(2.10) |
は

個より多くの解を有することはない.
解の数とは(
2.10)を満たす

を法とする剰余類の個数である.
■
証明
次数 に関する数学的帰納法で示す.
に関する数学的帰納法で示す.
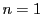 のとき.一次の合同方程式
のとき.一次の合同方程式
は定理12によって,  を法としてただ一つの解を有する.
を法としてただ一つの解を有する.
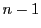 次のとき解が
次のとき解が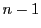 個以下であることが示されたとする.
(2.10)が解を有するときその一つを
個以下であることが示されたとする.
(2.10)が解を有するときその一つを
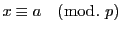 とする.
すなわち
とする.
すなわち
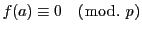 .
このとき多項式の除法の原理(定理37)によって
.
このとき多項式の除法の原理(定理37)によって
となる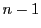 次の多項式
次の多項式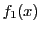 がある.
がある.
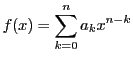 とおくと
とおくと
なので, 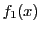 は整数が係数の多項式である.
このとき合同方程式(2.10)は
は整数が係数の多項式である.
このとき合同方程式(2.10)は
と同一の解を有する. が素数であるからこの合同式は
が素数であるからこの合同式は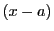 または
または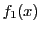 が
が で割り切れるときにかぎって成り立つ.
ゆえに
で割り切れるときにかぎって成り立つ.
ゆえに
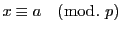 以外の解は
以外の解は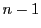 次の合同方程式
次の合同方程式
の解でなければならない.帰納法の仮定によりこの解は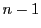 個以下である.
個以下である.
よって(2.10)の解は 個以下である.□
個以下である.□
さて一般の合同方程式
は, が素数の場合に解ければ,
が素数の場合に解ければ,
 を素因数分解して各因子を法とする方程式の解から
具体的に構成することが出来る.
を素因数分解して各因子を法とする方程式の解から
具体的に構成することが出来る.
それを二段階に分けて示そう.
まず, が素数
が素数 のべきつまり
のべきつまり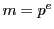 のときの解は,
のときの解は,
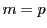 のときの解から帰納的に構成することが出来ることを示す.
そのために,
のときの解から帰納的に構成することが出来ることを示す.
そのために,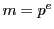 の解から
の解から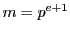 のときの解が構成できることを示す(定理15).
この定理によって,
のときの解が構成できることを示す(定理15).
この定理によって, のときから順次解を構成してゆくことによって,
のときから順次解を構成してゆくことによって,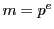 のときの解が構成できる.
のときの解が構成できる.
次に, が
が
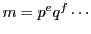 と因数分解されるときの解は,
と因数分解されるときの解は,
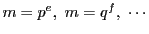 のときの解から構成することが出来ることを示す(定理16).
のときの解から構成することが出来ることを示す(定理16).
定理 15
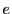
を自然数,

を素数とする.合同方程式
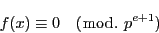 |
(2.11) |
の解は
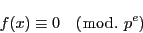 |
(2.12) |
の解から構成することが出来る.
証明
(2.11)の解は法を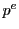 で考えることにより(2.12)を満たす.
よって
で考えることにより(2.12)を満たす.
よって が(2.11)の解であるために,
(2.12)の解
が(2.11)の解であるために,
(2.12)の解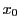 を用いて
を用いて
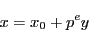 |
(2.13) |
と表されることが必要である.
逆に方程式(2.12)の各解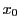 に対し(2.13)の形の数
に対し(2.13)の形の数 が
方程式(2.11)の解となるように
が
方程式(2.11)の解となるように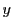 をとることができるか否かを判断し,
可能ならそれを求めることができる.
をとることができるか否かを判断し,
可能ならそれを求めることができる.
一般に整数係数の整式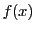 に対して
に対して
と展開され,さらに各
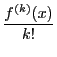 は
は の
の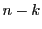 次の整数係数の整式で
あることに注意する.
次の整数係数の整式で
あることに注意する.
この に
に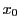 を,
を,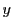 に
に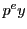 を代入することにより
を代入することにより
を得る.
上の注意から各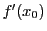 ,
,
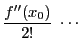 は整数である.
ゆえにこの展開式の第3項以下は
は整数である.
ゆえにこの展開式の第3項以下は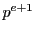 で割りきれる.
で割りきれる.
この結果合同方程式
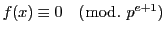 は
は
と同値である.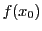 は
は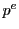 で割り切れるので
で割り切れるので
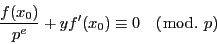 |
(2.14) |
ここで二つの場合を区別する.
(1)
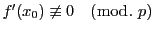 のとき.
このときは(2.14)は
のとき.
このときは(2.14)は を法としてただ一つの解をもつ.それを
を法としてただ一つの解をもつ.それを
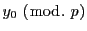 とする.
とする.
は(2.11)の解である.
(2)
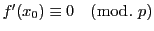 のとき.
このときは(2.14)は
のとき.
このときは(2.14)は
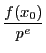 がさらに
がさらに で割り切れなければ解がない.
で割り切れなければ解がない.
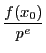 が
が で割り切れるなら
で割り切れるなら の剰余系の任意の
の剰余系の任意の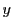 が解になる.つまり
が解になる.つまり
が(2.11)を満たす.
すなわち
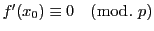 となる(2.12)の解
となる(2.12)の解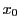 に対して,
(2.13)の形の数
に対して,
(2.13)の形の数 は,
は,
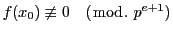 なら
なら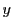 によらず(2.11)の解でなく,
によらず(2.11)の解でなく,
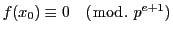 なら(2.11)の
なら(2.11)の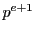 を法とする
を法とする 個の解を与える.
□
個の解を与える.
□
例 2.1.3
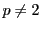
が素数で,

は

で割り切れないとする.そのとき
に解があるときは,その解は二つある.それを
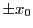
とする.
この場合には,
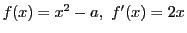
である.ゆえに
これは上定理の(1)の場合である.ゆえに
には二つの解がある.
例えば,
の解は
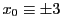
である.これから
の解を求めてみよう.そのために
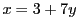
とおく.
定理 16
法

を素数べきに因数分解して
とするとき,
がそれぞれ
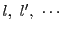
個の解をもつとすれば,
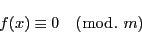 |
(2.17) |
は
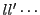
個の解をもつ.それは
から求められる.ここで
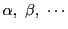
はそれぞれ
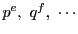
を法としての
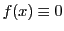
の任意の解の一組である.■
証明
 が(2.17)の解ならば(2.15),(2.16)の解である.
したがって(2.18)を満たす.
が(2.17)の解ならば(2.15),(2.16)の解である.
したがって(2.18)を満たす.
逆に(2.18)を満たす は,(2.15),(2.16)を満たすから,
(2.17)を満たす.□
は,(2.15),(2.16)を満たすから,
(2.17)を満たす.□
例 2.1.4
の解はそれぞれ二つある.それらを
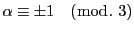
と
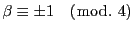
とする.
は四つの解をもつ.それらは,
から求められる.


 次: オイラーの関数
上: 合同式
前: 一次合同方程式
Aozora Gakuen
次: オイラーの関数
上: 合同式
前: 一次合同方程式
Aozora Gakuen
![]() に関する数学的帰納法で示す.
に関する数学的帰納法で示す.
![]() のとき.一次の合同方程式
のとき.一次の合同方程式
![]() 次のとき解が
次のとき解が![]() 個以下であることが示されたとする.
(2.10)が解を有するときその一つを
個以下であることが示されたとする.
(2.10)が解を有するときその一つを
![]() とする.
すなわち
とする.
すなわち
![]() .
このとき多項式の除法の原理(定理37)によって
.
このとき多項式の除法の原理(定理37)によって
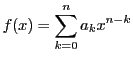 とおくと
とおくと
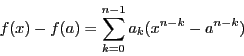
![]() 個以下である.□
個以下である.□
![]() が素数
が素数![]() のべきつまり
のべきつまり![]() のときの解は,
のときの解は,
![]() のときの解から帰納的に構成することが出来ることを示す.
そのために,
のときの解から帰納的に構成することが出来ることを示す.
そのために,![]() の解から
の解から![]() のときの解が構成できることを示す(定理15).
この定理によって,
のときの解が構成できることを示す(定理15).
この定理によって,![]() のときから順次解を構成してゆくことによって,
のときから順次解を構成してゆくことによって,![]() のときの解が構成できる.
のときの解が構成できる.
![]() が
が
![]() と因数分解されるときの解は,
と因数分解されるときの解は,
![]() のときの解から構成することが出来ることを示す(定理16).
のときの解から構成することが出来ることを示す(定理16).
![]() で考えることにより(2.12)を満たす.
よって
で考えることにより(2.12)を満たす.
よって![]() が(2.11)の解であるために,
(2.12)の解
が(2.11)の解であるために,
(2.12)の解![]() を用いて
を用いて
![]() に対し(2.13)の形の数
に対し(2.13)の形の数![]() が
方程式(2.11)の解となるように
が
方程式(2.11)の解となるように![]() をとることができるか否かを判断し,
可能ならそれを求めることができる.
をとることができるか否かを判断し,
可能ならそれを求めることができる.
![]() に対して
に対して
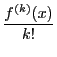 は
は![]() に
に![]() を,
を,![]() に
に![]() を代入することにより
を代入することにより
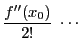 は整数である.
ゆえにこの展開式の第3項以下は
は整数である.
ゆえにこの展開式の第3項以下は![]() は
は
![]() のとき.
このときは(2.14)は
のとき.
このときは(2.14)は![]() を法としてただ一つの解をもつ.それを
を法としてただ一つの解をもつ.それを
![]() とする.
とする.
![]() のとき.
このときは(2.14)は
のとき.
このときは(2.14)は
![]() がさらに
がさらに![]() で割り切れなければ解がない.
で割り切れなければ解がない.
![]() が
が![]() で割り切れるなら
で割り切れるなら![]() の剰余系の任意の
の剰余系の任意の![]() が解になる.つまり
が解になる.つまり
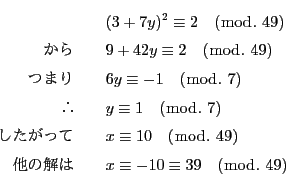
![]() が(2.17)の解ならば(2.15),(2.16)の解である.
したがって(2.18)を満たす.
が(2.17)の解ならば(2.15),(2.16)の解である.
したがって(2.18)を満たす.
![]() は,(2.15),(2.16)を満たすから,
(2.17)を満たす.□
は,(2.15),(2.16)を満たすから,
(2.17)を満たす.□