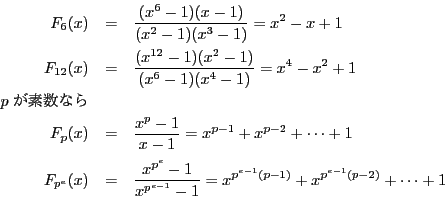次: フェルマの小定理
上: 1の
次: フェルマの小定理
上: 1の 乗根
前: 1の
乗根
前: 1の 乗根
乗根
1の  乗根,すなわち方程式
乗根,すなわち方程式
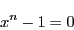 |
(2.24) |
の根は  個ある.それらは
個ある.それらは
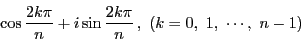 |
(2.25) |
である.これらはすべて偏角が異なり異なる複素数である.
しかも 乗すると1になるので,方程式(2.24)の解である.
したがってこの
乗すると1になるので,方程式(2.24)の解である.
したがってこの 個の複素数が
個の複素数が 次方程式(2.24)の根のすべてであることがわかる.
次方程式(2.24)の根のすべてであることがわかる.
簡単のために
とおく.ド・モアブルの定理より,(2.25)は
と表される.
ここで 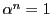 なので,(2.25)において
なので,(2.25)において  に与えるべき値は
に与えるべき値は
 を法としての一つの剰余系である.
さらに
を法としての一つの剰余系である.
さらに のとき
(2.25)において
のとき
(2.25)において
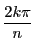 は
は  倍してはじめて
倍してはじめて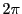 になるので,
になるので,
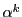 は
は  乗してはじめて 1 に等しくなる.
1の
乗してはじめて 1 に等しくなる.
1の  乗根のうち
乗根のうち  乗してはじめて 1 になるものを1の原始
乗してはじめて 1 になるものを1の原始  乗根という.
乗根という.
定理 21
1の原始

乗根は
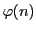
個ある.それらは
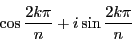 |
(2.26) |
において,

に

を法としての既約剰余系の値を与えて得られるものである.■
証明
すでに述べたように のとき
(2.26)の
のとき
(2.26)の
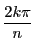 は
は  倍してはじめて
倍してはじめて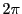 になるので,
になるので,
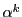 は
は  乗してはじめて 1 に等しくなる.つまり
乗してはじめて 1 に等しくなる.つまり 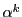 は
原始
は
原始  乗根である.
乗根である.
逆に 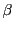 が原始
が原始  乗根であるとする.
乗根であるとする. 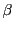 は
は 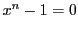 の根であるから
の根であるから
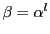 と表される.
と表される.
もし 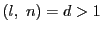 なら
なら 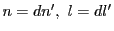 とおくとき
とおくとき
なので,
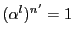 となり,
となり,  乗してはじめて1となるという仮定に反する.
ゆえに
乗してはじめて1となるという仮定に反する.
ゆえに 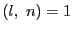 となる.
となる.
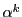 が原始
が原始  乗根となることと,
乗根となることと,
 と互いに素な
と互いに素な  を用いて
を用いて 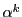 と表されることが同値であることが示された.
よってその個数は
と表されることが同値であることが示された.
よってその個数は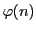 個である.□
個である.□
ちなみに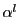 は原始
は原始 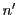 乗根である.これを次の定理22の証明に用いる.
乗根である.これを次の定理22の証明に用いる.
例 2.3.1
1の6乗根は
そのうち原始6乗根は最後の二つだけである.
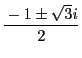
は原始3乗根,
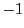
は原始2乗根,1は1乗根である.
定理 22

の素因数分解を
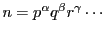
とし,
とすれば,
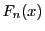
は1の原始

乗根のみを根とする多項式である.
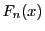
は
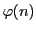
次で,その最高次数の係数は1,
その他の係数もすべて整数である.
ここに
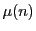
はメビウスの関数である.■
証明
1の原始  乗根のみを単根とする方程式で
最高次数の係数が1であるものを
乗根のみを単根とする方程式で
最高次数の係数が1であるものを 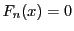 とする.
定理21の証明より,その他の
とする.
定理21の証明より,その他の  乗根は
乗根は
 の約数
の約数 に対し、原始
に対し、原始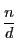 乗根になるが,
乗根になるが,
 が1以外の約数を動けば
が1以外の約数を動けば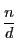 は
は
 以外の約数を動くので,原始
以外の約数を動くので,原始  乗根以外の
乗根以外の  乗根は
乗根は
 の真の約数
の真の約数  を次数とする原始
を次数とする原始  乗根になる.
原始
乗根になる.
原始  乗根と合わせた全体がちょうど
1の
乗根と合わせた全体がちょうど
1の 乗根の全体である.つまり
乗根の全体である.つまり
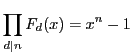 となる.
となる.
 を十分大きく各
を十分大きく各 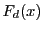 が正の値をとるように固定する.
それぞれの最高次数の係数が正なのでそれは可能である.
その上で両辺の対数をとる.
が正の値をとるように固定する.
それぞれの最高次数の係数が正なのでそれは可能である.
その上で両辺の対数をとる.
整数  と
と  に関する等式と見ればメビウスの反転公式(6節定理20)
が使え
に関する等式と見ればメビウスの反転公式(6節定理20)
が使え
つまり
両辺  の多項式で,十分大きい
の多項式で,十分大きい でつねに成立するので
でつねに成立するので
 に関して恒等的に成立する.したがって(2.28)が示された.
に関して恒等的に成立する.したがって(2.28)が示された.
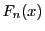 の次数は定理21より
の次数は定理21より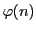 で
その係数は(2.28)より明らかに整数である.
式(2.27)の分子分母の最高次数の係数はともに1なので分母を払って
係数比較すれば
で
その係数は(2.28)より明らかに整数である.
式(2.27)の分子分母の最高次数の係数はともに1なので分母を払って
係数比較すれば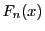 の最高次数の係数が1であることがわかる.□
の最高次数の係数が1であることがわかる.□


 次: フェルマの小定理
上: 1の 乗根
前: 1の 乗根
Aozora Gakuen
次: フェルマの小定理
上: 1の 乗根
前: 1の 乗根
Aozora Gakuen
![]() が原始
が原始 ![]() 乗根であるとする.
乗根であるとする. ![]() は
は ![]() の根であるから
の根であるから
![]() と表される.
と表される.
![]() なら
なら ![]() とおくとき
とおくとき
![]() が原始
が原始 ![]() 乗根となることと,
乗根となることと,
![]() と互いに素な
と互いに素な ![]() を用いて
を用いて ![]() と表されることが同値であることが示された.
よってその個数は
と表されることが同値であることが示された.
よってその個数は![]() 個である.□
個である.□
![]() は原始
は原始 ![]() 乗根である.これを次の定理22の証明に用いる.
乗根である.これを次の定理22の証明に用いる.
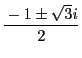 は原始3乗根,
は原始3乗根,
![]() 乗根のみを単根とする方程式で
最高次数の係数が1であるものを
乗根のみを単根とする方程式で
最高次数の係数が1であるものを ![]() とする.
定理21の証明より,その他の
とする.
定理21の証明より,その他の ![]() 乗根は
乗根は
![]() の約数
の約数![]() に対し、原始
に対し、原始![]() 乗根になるが,
乗根になるが,
![]() が1以外の約数を動けば
が1以外の約数を動けば![]() は
は
![]() 以外の約数を動くので,原始
以外の約数を動くので,原始 ![]() 乗根以外の
乗根以外の ![]() 乗根は
乗根は
![]() の真の約数
の真の約数 ![]() を次数とする原始
を次数とする原始 ![]() 乗根になる.
原始
乗根になる.
原始 ![]() 乗根と合わせた全体がちょうど
1の
乗根と合わせた全体がちょうど
1の![]() 乗根の全体である.つまり
乗根の全体である.つまり
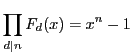 となる.
となる.
![]() を十分大きく各
を十分大きく各 ![]() が正の値をとるように固定する.
それぞれの最高次数の係数が正なのでそれは可能である.
その上で両辺の対数をとる.
が正の値をとるように固定する.
それぞれの最高次数の係数が正なのでそれは可能である.
その上で両辺の対数をとる.
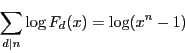
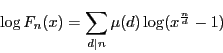
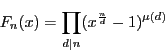
![]() の次数は定理21より
の次数は定理21より![]() で
その係数は(2.28)より明らかに整数である.
式(2.27)の分子分母の最高次数の係数はともに1なので分母を払って
係数比較すれば
で
その係数は(2.28)より明らかに整数である.
式(2.27)の分子分母の最高次数の係数はともに1なので分母を払って
係数比較すれば![]() の最高次数の係数が1であることがわかる.□
の最高次数の係数が1であることがわかる.□