ある整数![]() が整数
が整数![]() を法として平方剰余であるか平方非剰余であるかということと,整数
を法として平方剰余であるか平方非剰余であるかということと,整数![]() が整数
が整数![]() を法として平方剰余であるか平方非剰余であるかということとの間にはガウスが整数論の基本定理と呼んだ大変美しい定理が成り立つ.
それが 平方剰余の相互法則 である.
これはこの『数論初歩』全体でもいちばん山場の定理である.
を法として平方剰余であるか平方非剰余であるかということとの間にはガウスが整数論の基本定理と呼んだ大変美しい定理が成り立つ.
それが 平方剰余の相互法則 である.
これはこの『数論初歩』全体でもいちばん山場の定理である.
ぜひ高校生に「平方剰余の相互法則」を理解しその美しさを味わってもらいた
以下本節では ![]() は2以外の素数とする.
は2以外の素数とする.
![]() が解をもつとき
が解をもつとき ![]() を
を ![]() の平方剰余,
解がないとき平方非剰余という.
の平方剰余,
解がないとき平方非剰余という.
![]() である整数
である整数 ![]() に対して
に対して
![]() が
が ![]() の平方剰余であるか非剰余であるかにしたがって
の平方剰余であるか非剰余であるかにしたがって
![]() の任意の原始根を底として指数をとるとき,前節の議論から
の任意の原始根を底として指数をとるとき,前節の議論から
![]() が偶数なら
が偶数なら ![]() は平方剰余,奇数なら非剰余であった.ゆえに
は平方剰余,奇数なら非剰余であった.ゆえに
ゆえに ![]() に関する
に関する ![]() 個の既約類の中で半数は平方剰余のみからなり,
半数は非剰余のみからなる.
個の既約類の中で半数は平方剰余のみからなり,
半数は非剰余のみからなる.
![]() なので
なので
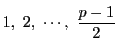 の
平方が平方剰余のすべてである.
また(3.1)から次の2性質が成り立つ.
の
平方が平方剰余のすべてである.
また(3.1)から次の2性質が成り立つ.
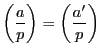
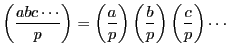
証明
ゆえに
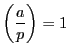 ならば,
ならば,
![]() で一致.
で一致.
また
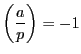 ならば,
ならば,
![]() .
ところがフェルマの小定理から
.
ところがフェルマの小定理から
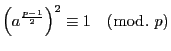 .
したがって
.
したがって
![]() でやはり一致する.□
でやはり一致する.□
この証明は,これまでの結果を結びつけただけであるが,より直接的な証明がディリクレの 『整数論講義』にある.『初等整数論講義』に従ってそれを紹介する.
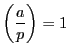 のとき.
のとき. ![]() を
を
![]() の解とすれば,
の解とすれば, ![]() の共役は
の共役は![]() 自身である.
自身である.
![]() もまた
もまた
![]() の解で,
の解で, ![]() の共役も
の共役も![]() である.
である.
![]() の元で
の元で
![]() を満たすものは定理14から
この二つ(
を満たすものは定理14から
この二つ( ![]() が奇数なので
が奇数なので![]() )にかぎる.この二つを除いた殘りの
)にかぎる.この二つを除いた殘りの ![]() 個は
二つずつ互いに共役で,それら
個は
二つずつ互いに共役で,それら ![]() 個の積は,
個の積は,
![]() となる.
となる.
![]() なので
なので
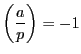 のときは共役と一致する数は
のときは共役と一致する数は 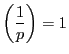 なので
なので
これをあわせると上記の場合分けは
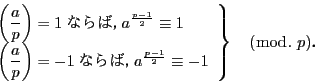
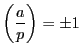 にかかわらず,
にかかわらず,
つまりこれはフェルマの小定理の別証になっている.
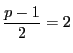 なのでオイラーの規準から
なのでオイラーの規準から