不定方程式
はガウス整数環のなかに
証明
背理法で示す.
![]() の解
の解
![]() があるとする.
があるとする.
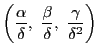 も解である.よってはじめから
も解である.よってはじめから
![]() がともに
がともに![]() の倍数でないとする.
補題7より,
の倍数でないとする.
補題7より,
![]() はともに
8の倍数なので,
はともに
8の倍数なので,
![]() は8の倍数である.
は8の倍数である.
![]() とおくと
とおくと
![]() となり
となり![]() が従って
が従って![]() は素数
は素数![]() の倍数である.
の倍数である.
![]() とおくと
とおくと
![]() となり,
となり,
![]() と2,つまりは
と2,つまりは![]() と
と![]() は互いに素である.
は互いに素である.
一方,
![]() は8の倍数である.つまり
は8の倍数である.つまり
![]() より
より![]() が4の倍数となる.
補題7より
が4の倍数となる.
補題7より![]() または
または![]() が4の倍数であり,
この結果
が4の倍数であり,
この結果![]() または
または![]() が4の倍数となって,矛盾である.
が4の倍数となって,矛盾である.
よって![]() と
と![]() の一方のみが
の一方のみが![]() の倍数である.
の倍数である.
![]() と
と![]() について対称なので
について対称なので
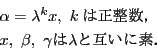
ここで
![]() なので,
なので,
![]() が
が![]() の倍数であることと
の倍数であることと
![]() が
が
![]() の倍数であることは同値である.よって等式(4.3)となるためにはともに
の倍数であることは同値である.よって等式(4.3)となるためにはともに![]() の倍数でなければならない.つまり
の倍数でなければならない.つまり![]() である.よってまた
である.よってまた
![]() が
が![]() の倍数であるが
の倍数であるが![]() の倍数ではなく,
の倍数ではなく,
![]() が
が
![]() の倍数であるとして良い.逆の場合は
の倍数であるとして良い.逆の場合は![]() に代えて
に代えて![]() で考えればよい.よって等式(4.3)より
で考えればよい.よって等式(4.3)より
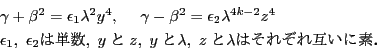
![]() を示す.
を示す.![]() とする.このとき等式(4.5)の右辺の各項は
奇数なので和は偶数,つまり
とする.このとき等式(4.5)の右辺の各項は
奇数なので和は偶数,つまり![]() の倍数となる.これは
の倍数となる.これは![]() が
が![]() と互いに素であることに反する.よって
と互いに素であることに反する.よって![]() である.
である.
等式(4.5)において![]() であるから
であるから
![]() は
は![]() の倍数.つまり4の倍数である.
の倍数.つまり4の倍数である.
一方,![]() も
も![]() も
も![]() の倍数ではないので,補題7とその証明より
の倍数ではないので,補題7とその証明より![]() または
または![]() が4の倍数で,
が4の倍数で,![]() は8の倍数である.
は8の倍数である.![]() が4の倍数のときは
が4の倍数のときは![]() が4の倍数になる.
よって
が4の倍数になる.
よって![]() が4の倍数としてよく,このとき
が4の倍数としてよく,このとき![]() が4の倍数になる.
が4の倍数になる.
![]() は単数なので
は単数なので![]() である.このとき等式(4.5)は単数
である.このとき等式(4.5)は単数![]() をもちいて
をもちいて
よって帰納的に![]() でも成立するが,これは
でも成立するが,これは![]() という先に示した結果と矛盾する.
よって等式(4.3)をみたす
という先に示した結果と矛盾する.
よって等式(4.3)をみたす
![]() は存在しない.
□
は存在しない.
□
この定理からただちに次の結論が導かれる.