 「格子」という言葉の意味を知らない人も多いと思われるので,
平安時代の「格子」のある絵を紹介する.
「格子」という言葉の意味を知らない人も多いと思われるので,
平安時代の「格子」のある絵を紹介する.
 「格子」という言葉の意味を知らない人も多いと思われるので,
平安時代の「格子」のある絵を紹介する.
「格子」という言葉の意味を知らない人も多いと思われるので,
平安時代の「格子」のある絵を紹介する.
「格子」とはもともとこのように細い角材を縦横に組み合わせて作った建具. 寝殿造りの建具である蔀(しとみ)のこと. 『竹取物語』に「かうし共も、人はなくしてあきぬ」 などとある.さらに細い木や竹などを、縦横に間をすかして組んで、 窓や戸口の外などに打ちつけたものをいう.
このような格子点を最初に研究したのはガウス(Gauss,1777-1855) である.それを引き継ぎ 整数問題の各方面に応用したのが,ミンコフスキー(H.Minkowski,1864-1909)である. 彼はドイツの幾何学者であり,幾何学的考察を整数論に適用して『数の幾何』なる分野を開拓した.
![]() 座標平面の点で
座標平面の点で![]() 座標,
座標,![]() 座標とも整数である点を格子点という.
座標とも整数である点を格子点という.
これを拡張した次の定理を証明する.
証明
図形 ![]() を
を ![]() 平面上に置く.
平面上に置く. ![]() と
と ![]() を任意の整数とし,図形
を任意の整数とし,図形 ![]() を直線群
を直線群 ![]() を引き,いくつかの一辺の長さ1の正方形に含まれる小領域に分割する.分割の境界は分割された双方に入れる.
を引き,いくつかの一辺の長さ1の正方形に含まれる小領域に分割する.分割の境界は分割された双方に入れる.
小領域を含むこれらの正方形をおのおの平行に移動し,一つの正方形の上に重ねる.このとき ![]() の面積が
の面積が ![]() であるから,一般に
であるから,一般に ![]() より多くの小領域が重なっている点が存在する.なぜならもしどの点での重なりも
より多くの小領域が重なっている点が存在する.なぜならもしどの点での重なりも ![]() より少なければ,一辺の長さが1の正方形を十分細かな小片に細分して,各小片上の重なりが
より少なければ,一辺の長さが1の正方形を十分細かな小片に細分して,各小片上の重なりが ![]() より少なくできる.従ってそれらの面積の総和も
より少なくできる.従ってそれらの面積の総和も ![]() より小さくなるからである.
より小さくなるからである.![]() が整数のとき分割された境界でのみ重なりが
が整数のとき分割された境界でのみ重なりが ![]() を越えることがあり得るが,この場合はその境界上の点をとる.
を越えることがあり得るが,この場合はその境界上の点をとる.![]() が整数で,領域が正方形
が整数で,領域が正方形 ![]() 枚ちょうどからできているときにかぎり,
枚ちょうどからできているときにかぎり, ![]() 個の点の重なりしかないがこの場合ははじめから平行移動する必要がない.
個の点の重なりしかないがこの場合ははじめから平行移動する必要がない.
従って自明な最後の場合を除き,領域の重なりが ![]() より大きい点が存在する.そのときの重なりの個数を
より大きい点が存在する.そのときの重なりの個数を ![]() とする.
とする. ![]() である.
である.
この点を分割された各正方形に記し,これらの正方形を元の位置に戻す.すると ![]() 上に
点列
上に
点列
![]() ができ,これらの任意の2点間の
ができ,これらの任意の2点間の![]() 座標,
座標, ![]() 座標の差はどれも整数である.
座標の差はどれも整数である.![]() が格子点に来るように平行移動させれば,
が格子点に来るように平行移動させれば,
![]() はすべて格子点である.□
はすべて格子点である.□
これをもとに定理52を証明しよう.
証明
図形 ![]() は,面積が4で,原点
は,面積が4で,原点 ![]() を対称の中心とするとしてよい.
を対称の中心とするとしてよい.
![]() を中心に
を中心に ![]() を 長さで
を 長さで![]() に縮小した図形を
に縮小した図形を ![]() とする.
とする.
![]() は面積が1であるから,
は面積が1であるから, ![]() の内部あるいは周上に,2点
の内部あるいは周上に,2点
![]() と
と
![]() で,その差
で,その差 ![]() がともに整数であるものが存在する.
がともに整数であるものが存在する.
![]() も
も ![]() に関して対称であるから,
に関して対称であるから, ![]() の対称点
の対称点
![]() も
も![]() の周か内部にある.さらに
の周か内部にある.さらに ![]() も凸形であるから
も凸形であるから ![]() が
が ![]() に含まれ,特にその中点
に含まれ,特にその中点
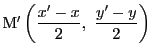 も
も ![]() に含まれる.
に含まれる.![]() と
と ![]() は異なる点なので
は異なる点なので ![]() は
は ![]() と異なる.
と異なる.
そこで ![]() を2倍に拡大した点を
を2倍に拡大した点を ![]() とすれば
とすれば ![]() は
は ![]() の周か内部にあり,
の周か内部にあり,
![]() であるから確かに格子点である.
□
であるから確かに格子点である.
□
実数を有理数で近似するという問題に関して,ミンコフスキーの定理は非常に有効である.
証明
この連立不等式が定める領域を ![]() とする.
とする. ![]() に点
に点 ![]() が属すれば
が属すれば ![]() も属するから原点対称である.
も属するから原点対称である.
![]() の面積は
の面積は
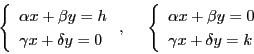
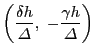 ,
,
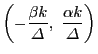 である.したがって
である.したがって
証明
定理54において,
![]() とすれば
とすれば
![]() である.よって
である.よって
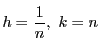 とすれば,
とすれば,