整数![]() に対してベクトル
に対してベクトル
ここで, ![]() を整数としさらに
を整数としさらに ![]() であるとする.
正方格子の格子点
であるとする.
正方格子の格子点
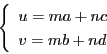
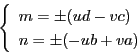
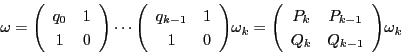
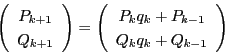
![]() 座標と正方格子を準備する.
座標と正方格子を準備する.
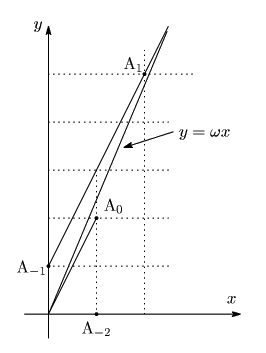 まず直線
まず直線 ![]() を描く.この直線を
を描く.この直線を ![]() と呼ぶ.
と呼ぶ.
![]() とおく.直線
とおく.直線 ![]() 上,
上, ![]() を越えない
を越えない ![]() 座標最大の格子点が
座標最大の格子点が
![]() である.
次に
である.
次に
![]() を通り,
を通り,
![]() に平行な直線
に平行な直線
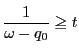 を満たす最大の整数
を満たす最大の整数
この ![]() を
を ![]() とおく.
このときその格子点が
とおく.
このときその格子点が ![]() である.つまり
である.つまり
![]() が定まったときに
直線
が定まったときに
直線
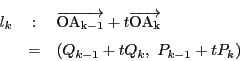

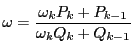 であるから,
であるから,
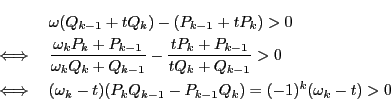
![]() から
から![]() を与える
を与える![]() までの各
までの各![]() の値に対して
順次線分
の値に対して
順次線分
![]() 上の格子点が定まり,これ以外にはない.
上の格子点が定まり,これ以外にはない.
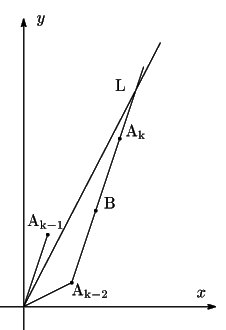
このように直線
![]() の傾きは
の傾きは ![]() の傾きに近づき,
の傾きに近づき,
![]() の両側にできる二つの折れ線
の両側にできる二つの折れ線
![]() と
と
![]() の間には格子点が一つも存在しない.
の間には格子点が一つも存在しない.
格子点 ![]() は,
は,![]() と
と ![]() に関して同じ側にありその
に関して同じ側にありその ![]() 座標が
座標が![]() の
の ![]() 座標より小さいどの格子点より,
座標より小さいどの格子点より, ![]() に近い.
に近い.
このことを定式化することにより次の定理が得られる.
定理 55
![]() は与えられた無理数,
は与えられた無理数, ![]() は与えられた2より大きい正の定数であり,
整数
は与えられた2より大きい正の定数であり,
整数![]() は
は![]() にあるとする.
にあるとする.
証明
線分
![]() の長さは線分
の長さは線分
![]() の長さの整数倍であるから,
の長さの整数倍であるから,
したがって題意をみたす格子点は ![]() のなかで
のなかで
![]() 座標が
座標が ![]() を超えない最大のものによって与えられる.□
を超えない最大のものによって与えられる.□
一次形式 ![]() において
において![]() と
と![]() は整数値のみをとるとし,さらに
は整数値のみをとるとし,さらに![]() とする.
このときこの一次形式の絶対値はいくらでも小さくすることができた.
つまり無理数
とする.
このときこの一次形式の絶対値はいくらでも小さくすることができた.
つまり無理数 ![]() は有理数
は有理数
![]() で
で
格子点の理論を用いて,無理数の近似の程度に関するさらに詳しい結果を紹介しよう.
証明
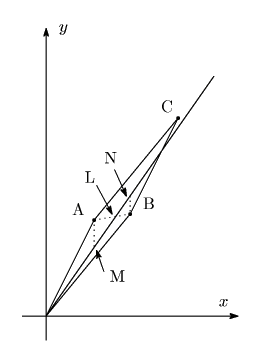
![]() と
と
![]() を隣りあう二つの近似分数に対応する格子点とする.平行四辺形
を隣りあう二つの近似分数に対応する格子点とする.平行四辺形 ![]() を作る.
を作る. ![]() とすれば
とすれば ![]() が
が ![]() よりも
よりも ![]() 線に近い(
線に近い(
![]() ).ゆえに
).ゆえに
![]() が成り立つ.
が成り立つ.
しかるに