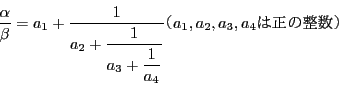
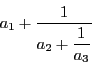
自然数![]() に対して,
に対して,![]() と
と![]() を
を
![]() を正の無理数とする.
を正の無理数とする. ![]() とおく.
とおく. ![]() に対して,
に対して, ![]() を超えない最大の整数を
を超えない最大の整数を ![]() とおき,
とおき,
また, 数列
![]() ,
,
![]() を次の漸化式で定義する.
を次の漸化式で定義する.
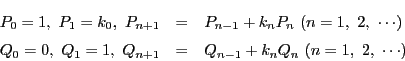
このとき次のことが成り立つことを示せ.
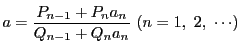
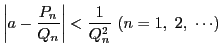
座標平面において, ![]() がともに整数であるような点
がともに整数であるような点 ![]() を格子点と呼ぶことにする.
この平面上で
を格子点と呼ぶことにする.
この平面上で
![]() は自然数で,
は自然数で,
![]() ,
,
![]() ,
,
![]() ,
,
![]() とする.これらを頂点とする
平行四辺形
とする.これらを頂点とする
平行四辺形 ![]() の周を除いた内部を
の周を除いた内部を ![]() とするとき,
とするとき,
![]() 平面において,
平面において, ![]() 座標,
座標, ![]() 座標ともに整数であるような点を格子点と呼ぶ.
格子点を頂点にもつ三角形
座標ともに整数であるような点を格子点と呼ぶ.
格子点を頂点にもつ三角形 ![]() を考える.
を考える.