二次無理数の理論は,あまり他の知識を必要とせず理解できる大変美しい理論であるが,殘念ながら高校では習わない.ぜひ意慾的な高校生が,実際に計算をしながら学び理解してほしい.
証明
なぜなら,![]() が
が![]() 解であるとして,
さらに
解であるとして,
さらに
![]() の解でもあるとする.
の解でもあるとする.
![]() を有理数とし,
を有理数とし,![]() とする.
とする.
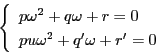
二次無理数![]() に対し,
に対し,
![]() が属する二次方程式のもう一つの根を
が属する二次方程式のもう一つの根を![]() の共役根と呼ぶ.
の共役根と呼ぶ.
証明
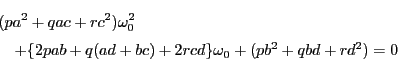
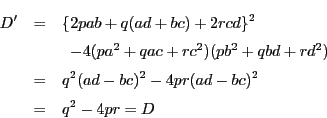
ここで,最も重要な論点となる定理を証明しよう.
それは 二次実無理数の連分数展開は循環する ということである.
既出の例5.2.1のように,![]() は第二項目から循環し,循環の長さは1である.このような循環性がすべての実二次無理数で成り立つのである.
は第二項目から循環し,循環の長さは1である.このような循環性がすべての実二次無理数で成り立つのである.
その証明のための次の事実に注意しよう.
証明
なぜなら,![]() より
より![]() .従って
.従って![]() は有限個である.
各
は有限個である.
各![]() に対して,
に対して,![]() を満たす整数の組
を満たす整数の組![]() は,
右辺の因数分解を4と
は,
右辺の因数分解を4と![]() と
と![]() に分ける場合の数なので有限個である.
□
に分ける場合の数なので有限個である.
□
証明
いくつかの段階に分けて考えよう.正のもので証明できればよく,また共役なもののいずれかで証明できればよいので![]() を正な二次無理数で,
を正な二次無理数で,![]() をその共役無理数とし,
をその共役無理数とし,
![]() とする.
とする.
等式6.1で![]() の共役をとると,
の共役をとると,
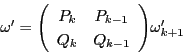
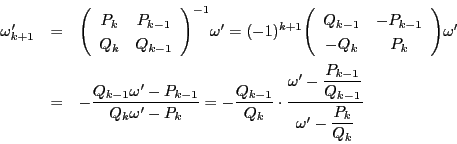
他方![]() は
は![]() から整数部分を除いた小数部分の逆数なので
から整数部分を除いた小数部分の逆数なので
![]() である.
さらに
である.
さらに
![]() とすれば
とすれば
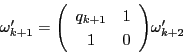
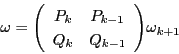
これら無理数の二次方程式は補題9より,
係数の定数倍を除いて一意なので,係数は互いに素としてよい.
これらの二次方程式は,二つの根の積が負で判別式が同一なので,
補題10の条件を満たす.補題10より
![]() の中に異なるものは有限個しかない.
の中に異なるものは有限個しかない.
ゆえにある番号![]() と
と![]() があって,
があって,
それを示す.
一般に一列に並んでいる数学的な対象が![]() 回毎にくり返しさらに
回毎にくり返しさらに![]() 回毎にくり返せば
回毎にくり返せば![]() 回毎にもくり返す.
なぜなら
回毎にもくり返す.
なぜなら![]() 回目のその対象を
回目のその対象を![]() と書けば,
と書けば,
![]() がつねに成立することから,
がつねに成立することから,
![]() を循環のはじまる番号とし,番号
を循環のはじまる番号とし,番号![]() は
は![]() とする.
番号
とする.
番号![]() は循環部分にあるので,
つまり
は循環部分にあるので,
つまり
![]() なる
なる![]() が存在する.
また,
が存在する.
また,
![]() も成立している.
も成立している.
さて,
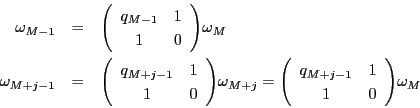
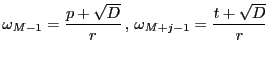 ,
とおけ,
,
とおけ,
逆に十分大きい![]() では
では
![]() となるので,
循環する部分は
となるので,
循環する部分は
![]() を満たしていなければならない.
を満たしていなければならない.
よって,循環のはじまる 番号![]() は
は
![]() となる最小の番号である.
□
となる最小の番号である.
□
![]() のことを二次無理数の連分数展開の周期と呼ぶ.
のことを二次無理数の連分数展開の周期と呼ぶ.

![]() の共役が条件を満たす最初の共役無理数である.実際
の共役が条件を満たす最初の共役無理数である.実際
![]() となり,ここから循環が始まっている.
そして循環周期は
となり,ここから循環が始まっている.
そして循環周期は![]() である.
である.