 が奇数の時
が奇数の時
- 正の偶数
 に対して,
に対して,
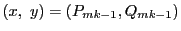 は
は
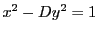 の解である.
の解である.
- 正の奇数
 に対して,
に対して,
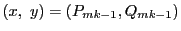 は
は
 の解である.
の解である.
- 正の偶数
 が偶数の時
が偶数の時
- 正整数
 に対して,
に対して,
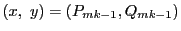 は
は
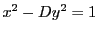 の解である.
の解である.
- 正整数
証明
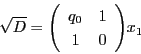
なぜなら,![]() は明らかであるが,
は明らかであるが,![]() を
を![]() を超えない最大の整数とすれば,
を超えない最大の整数とすれば,
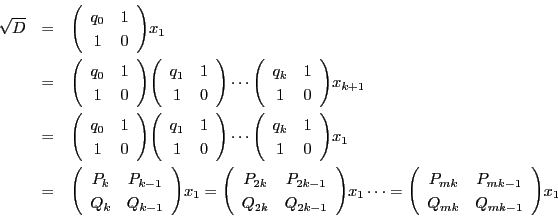
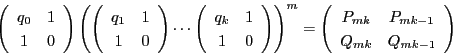
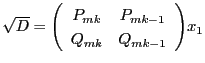 に,
に,
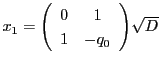 を代入する.
を代入する.
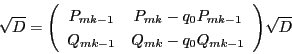
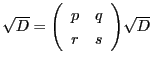 ならば,
ならば,
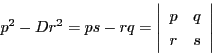
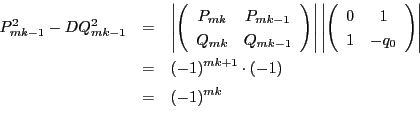
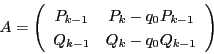
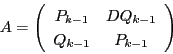
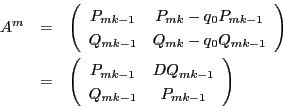
これでペル方程式の解の構造定理に現れる行列
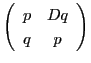 との関連も明確である.
との関連も明確である.
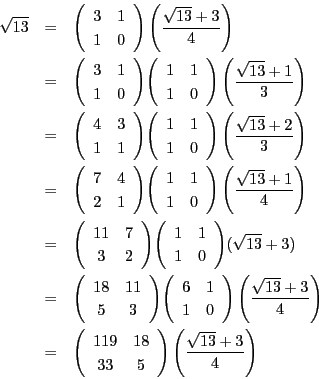
![]() が
が![]() の解となり
の解となり
![]() が
が![]() の解
となるはずである.
の解
となるはずである.
![]() である.
である.![]() を求める,
を求める,
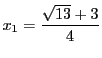 が次に
現れるときである.その展開は
が次に
現れるときである.その展開は
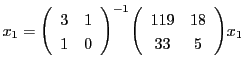 をあらためて
をあらためて
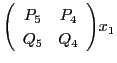 に代入する.
に代入する.
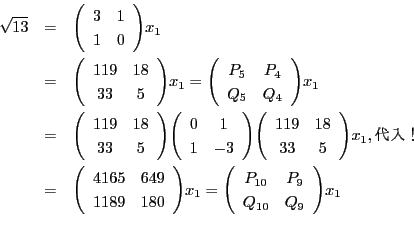
こうして
![]() の解が構成された.
実際,
の解が構成された.
実際,
残された最後の問題は,
ペル方程式の正の解がすべて
![]() から得られることを示すことである.この証明を一般の場合に示す.
から得られることを示すことである.この証明を一般の場合に示す.
証明
![]() である任意の解を
である任意の解を![]() とする.
とする.
![]() ,つまり
,つまり
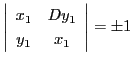 である.
ここで,
である.
ここで,
![]() であるので,ペル方程式の解の構造定理
57
の証明のなかで示したように,
であるので,ペル方程式の解の構造定理
57
の証明のなかで示したように, ![]() である.
である.
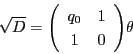
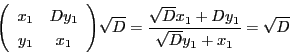
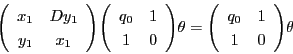
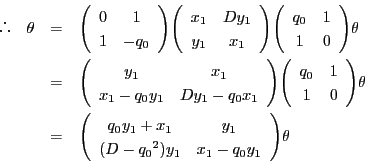
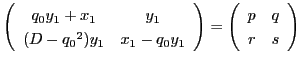 とおく.
とおく.
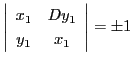 なので
なので![]() である.
である.
![]() とし,
とし,
![]() で
で
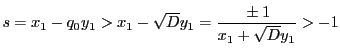 となるから,
となるから,![]() とあわせて,
とあわせて, ![]() である.
である.
さらに,
![]() は
は
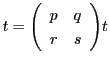 つまり
つまり
![]() の二根である.
の二根である.
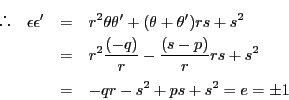
よって![]() .
さらに,
.
さらに,
![]() つまり
つまり
![]() が成り立つ.
したがって
が成り立つ.
したがって
そこで
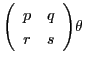 は
は
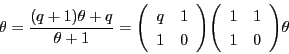
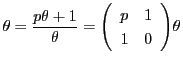
いずれの場合も
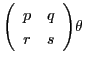 は
は![]() 自身の連分数展開のなかに現れる.
つまり
自身の連分数展開のなかに現れる.
つまり
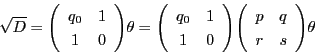
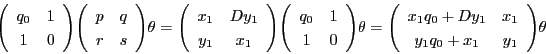
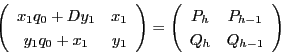
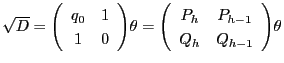 となり,
となり,
したがって,
![]() となり,題意が証明された.□
となり,題意が証明された.□
有理数体![]() に二次無理数
に二次無理数![]() をつけ加え四則演算で得られる数の集合は体をなす.これを
をつけ加え四則演算で得られる数の集合は体をなす.これを
![]() と書く.このなかで二次の項の係数が1である整数係数の二次方程式の解となっている数を
と書く.このなかで二次の項の係数が1である整数係数の二次方程式の解となっている数を
![]() の整数といい,その集合を整数環という.
の整数といい,その集合を整数環という.
ペルの方程式は,この整数環の単数を求めることに関連している.したがってペル方程式の数論的な性質を解明するためには二次体の数論が必要なのである.しかしそれは『数論初歩』の範囲を越えるので,これを指摘するにとどめる.