![]() に対して
に対して
![]() の
の
![]() のなかでの最小解を求める手順
は次の通りである.
のなかでの最小解を求める手順
は次の通りである.
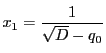 と置く.
と置く.
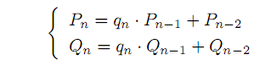
この手順を実行するプログラム言語を探す.
高等学校の教科書に載っている BASIC は,
数値が一定の桁の有効数字をもつ小数表示の近似実数である.
![]() と置けば,
と置けば,
![]() となる.
大きい数も有効桁までしか正しく表示されない.
従ってこのままでは
となる.
大きい数も有効桁までしか正しく表示されない.
従ってこのままでは![]() の判断ができない.
の判断ができない.
UBASIC という, BASIC を改良し,大きい整数も不動点表示をせずそのまま
で扱え,有理数も分母分子を(約分して)別々に保持するようにした言語がある.
それを用いる.// が分数である. UBASIC でも無理数は近似数になり,そのままでは
比較できないので,![]() の判断をさせるために,
の判断をさせるために,
![]() と
二つの有理数に分けそれぞれを比較することにする.
と
二つの有理数に分けそれぞれを比較することにする.
三項間漸化式を解くのには工夫がいる.![]() ,
,![]() の値を順次入れていく変数を二つずつ
用意し交互に用いるようにする.
の値を順次入れていく変数を二つずつ
用意し交互に用いるようにする.
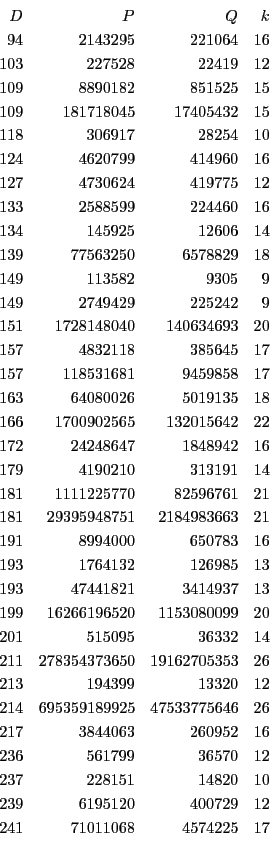
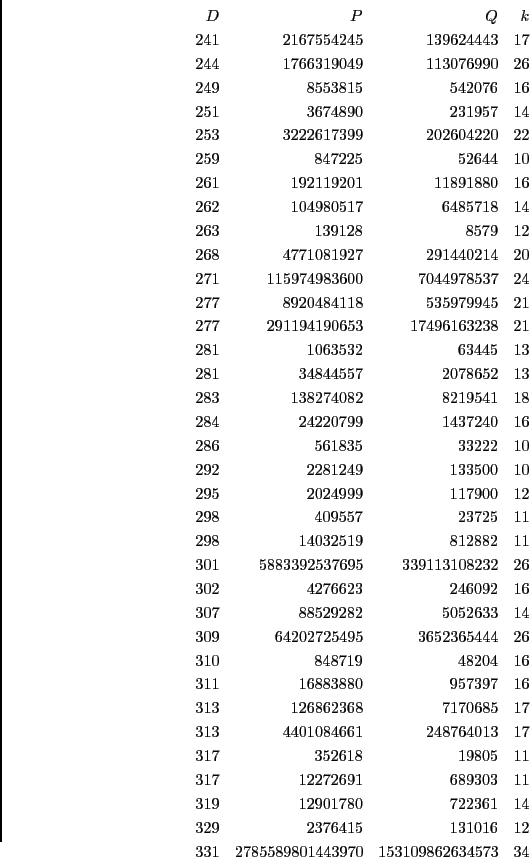
次に掲げるのは ![]() から
から ![]() まで,
まで,
![]() の
最小解を書き出すプログラムである.
の
最小解を書き出すプログラムである.
10 open "pell.txt" for create as #1 20 for D=2 to 1999 30 if D=(isqrt(D))^2 then 220 else 40 40 Q0=isqrt(D) 50 S1=Q0//(D-Q0^2):T1=1//(D-Q0^2) 60 X=S1+T1*(sqrt(D)):PA=Q0:QA=1:PB=1:QB=0:S=S1:T=T1 70 Q=int(X):PB=PA*Q+PB:QB=QA*Q+QB 80 K=K+1 90 S0=S 100 S=(Q-S)//(T^2*D-(Q-S)^2):T=T//(T^2*D-(Q-S0)^2) 110 X=S+T*(sqrt(D)) 120 if S=S1 and T=T1 then goto 190 else 130 130 Q=int(X):PA=PB*Q+PA:QA=QB*Q+QA 140 K=K+1 150 S0=S 160 S=(Q-S)//(T^2*D-(Q-S)^2):T=T//(T^2*D-(Q-S0)^2) 170 X=S+T*(sqrt(D)) 180 if S=S1 and T=T1 then goto 200 else 70 190 print #1,"&",PA,"&",QA,"&",K:goto 210 200 print #1,"&",PB,"&",QB,"&",K 210 K=0 220 next D 230 end