100までだと規則性があるようには見えない.1000になると少し上に凸な曲線に見え,
1000000となるとやや上に凸なきれいな曲線である.この曲線は対数のグラフに似ているではないか.このようなことをふまえて多くの人が![]() の性質を研究した.
の性質を研究した.
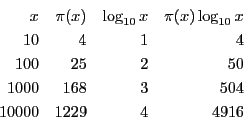
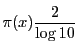 になるということである.
になるということである.
このようなことを昔の人はいろいろ調べた.計算機のない時代には手計算で調べた.![]() は約
は約![]() なのでこの計算では
なのでこの計算では
![]() はほぼ
はほぼ![]() ということになる.もっと
ということになる.もっと![]() を大きくとるとどのような値に収束するか,これをいろいろと推測したのだ.その結果1801年にルジャンドルは
を大きくとるとどのような値に収束するか,これをいろいろと推測したのだ.その結果1801年にルジャンドルは
この分野で実質的に最初の前進をしたのがロシアのチェビシェフである. かれは1850年に次のことを示した.先のページには次のように書かれている.
Tchebycheff made the first real progress toward a proof of the prime number theorem in 1850, showing there exist positive constantssuch that
and that ifhad a limit, then its value must be one.
ここで述べられているチェビシェフの定理の前半は,初等的に示すことができる.
これを示すためにひとつ補題を証明する.
証明
![]() は
は![]() となる最大の
となる最大の![]() の値である.
の値である.
1から![]() までの自然数のなかでちょうど
までの自然数のなかでちょうど![]() で割り切れるものの個数は
で割り切れるものの個数は
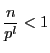 となり
となり
![$\left[\dfrac{n}{p^l} \right]=0$](images/img2704.gif) である.したがって求める個数は
である.したがって求める個数は
![\begin{eqnarray*}
&&\sum_{l=1}^{[\log_pn]}
l\left(\left[\dfrac{n}{p^l} \right]...
...right]\\
&=&\sum_{l=1}^{[\log_pn]}\left[\dfrac{n}{p^l}\right]
\end{eqnarray*}](images/img2705.gif)
定理65の証明
![]() を正整数として,整数
を正整数として,整数
![]() である素数に対して
である素数に対して
![]() の素因数分解に含まれる素数
の素因数分解に含まれる素数 ![]() の個数は,
補題13より
の個数は,
補題13より
![\begin{displaymath}
\sum_{l=1}^{[\log_p(2m)]}\left(\left[\dfrac{2m}{p^l} \right]-2\left[\dfrac{m}{p^l}\right]\right)
\end{displaymath}](images/img2710.gif)
![\begin{displaymath}
\left[\dfrac{2m}{p^l} \right]-2\left[\dfrac{m}{p^l}\right]=...
...iggl( \dfrac{p^l}{2}\le r <p^l \biggr)
\end{array}
\right.
\end{displaymath}](images/img2711.gif)
![\begin{displaymath}
\sum_{l=1}^{[\log_p(2m)]}\left(\left[\dfrac{2m}{p^l} \right...
...eft[\dfrac{m}{p^l}\right]\right)
\le \left[\log_p(2m)\right]
\end{displaymath}](images/img2712.gif)
![\begin{displaymath}
\dfrac{(2m)!}{m!m!}\le \prod_{p \le 2m}p^{[\log_p(2m)]}
\end{displaymath}](images/img2713.gif)
![\begin{displaymath}
\prod_{p \le 2m}p^{[\log_p(2m)]}\le (2m)^{\pi(2m)}
\end{displaymath}](images/img2715.gif)
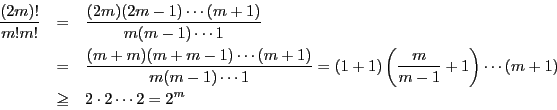
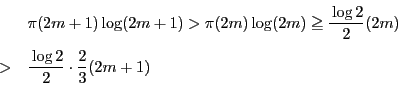
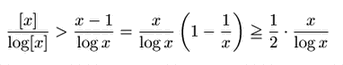
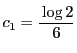 とおけばよい.
とおけばよい.
次に,
![]() の範囲の素数は
の範囲の素数は
![]() の分母を割らない.よって
の分母を割らない.よって
![]() は
は
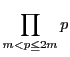 で割り切れる.つまり
で割り切れる.つまり
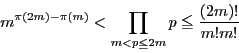
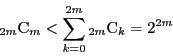
![\begin{eqnarray*}
\pi(2y)-\pi(y)&=&\pi([2y])-\pi([y])\\
&\le&\pi(2[y]+2)-\pi(...
...
&<&2\log 2\dfrac{[y]}{\log [y]}+2<(2\log 2+2)\dfrac{y}{\log y}
\end{eqnarray*}](images/img2741.gif)
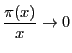 である.
である.
チェビシェフはさらにこの![]() を調べ,
を調べ,
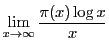 が収束するならば,
それは1であることも示した.
が収束するならば,
それは1であることも示した.