この証明のために次の等式を補題としてあらかじめ示しておこう.
証明
![]() に関する数学的帰納法で証明する.
に関する数学的帰納法で証明する.
![]() のときは
のときは
![]() のなかで
のなかで ![]() の倍数は
の倍数は
![]() のとき
のとき![]() が成立するとする.
が成立するとする.
![]() とし,さらに
とし,さらに ![]() が追加されたとする.
このときは,さらに
が追加されたとする.
このときは,さらに ![]() の倍数
の倍数
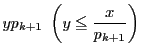 を除かなければならない.そのうち
を除かなければならない.そのうち ![]() が
が
![]() で割り切れるものは
すでに除かれているので,新たに除くべきものの個数は,
で割り切れるものは
すでに除かれているので,新たに除くべきものの個数は,
![]() を越えない整数のなかで
を越えない整数のなかで
![]() で割り切れないものの個数である.ゆえに求める個数
で割り切れないものの個数である.ゆえに求める個数![]() は
は
![\begin{eqnarray*}
N_{k+1}&=&[x]-\left[\dfrac{x}{p_1} \right]-\left[\dfrac{x}{p...
...ots
+(-1)^{k+1}\left[ \dfrac{x}{p_1p_2\cdots p_{k+1}}\right]
\end{eqnarray*}](images/img2643.gif)
さらに微積から補題をもう一つ.
証明
関数![]() は単調減少なので
区間
は単調減少なので
区間![]() で
で
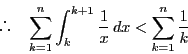
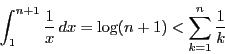
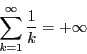
以上の準備をして定理64を証明しよう.
定理64の証明
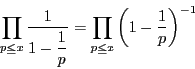
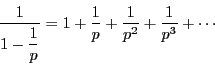
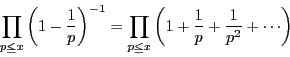
ここで補題12より,![]() のとき
のとき![]() の右辺は発散する.
の右辺は発散する.
もし
![]() が有限であれば,
が有限であれば,![]() のとき
のとき![]() の左辺は
有限個の素数にわたる和となり収束する.
これは矛盾なので
の左辺は
有限個の素数にわたる和となり収束する.
これは矛盾なので
![]() が示された.
が示された.
![\begin{eqnarray*}
\pi(x)&\le&r+[x]
-\left[\dfrac{x}{p_1}\right]-\left[\dfrac...
...ght]-\cdots
+(-1)^r\left[\dfrac{x}{p_1p_2\cdots p_r}\right]
\end{eqnarray*}](images/img2662.gif)
補題11の和の項数は![]() である.
である.
![]() なので,あわせて
なので,あわせて
![]() がなりたつ.
したがって
がなりたつ.
したがって
![\begin{eqnarray*}
&&[x]-\left[\dfrac{x}{p_1}\right]-\left[\dfrac{x}{p_2}\right...
...s p_r}\\
&=&2^r+x\prod_{k=1}^r\left(1-\dfrac{1}{p_k}\right)
\end{eqnarray*}](images/img2666.gif)
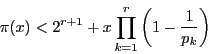
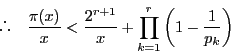
ここで![]() を
を
![]() である最大のものにとる.このとき
である最大のものにとる.このとき
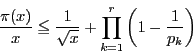
![]() のとき
のとき![]() である.したがって(1)で示したように
である.したがって(1)で示したように
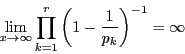
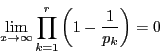
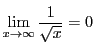 とあわせて
とあわせて