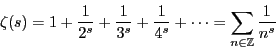
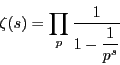
定理64の証明は![]() が発散することから,素数が無数に存在することを示したのである.
が発散することから,素数が無数に存在することを示したのである.
自然数全体にわたる和が,素数全体にわたる積と一致する.このことは素数の分布を調べることと,![]() 関数の性質を調べることのあいだに深い関係がることを意味している.
関数の性質を調べることのあいだに深い関係がることを意味している.
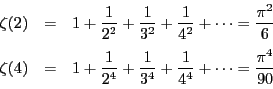
リーマンは![]() 関数を,複素関数として研究し時代を画する論文を残した.その中には今日もまだ未解決の問題が提起されている.
関数を,複素関数として研究し時代を画する論文を残した.その中には今日もまだ未解決の問題が提起されている.![]() は整数論できわめて重要であるばかりでなく,その他の分野でも頻繁に登場する.彼らの素数定理の証明はこのリーマンの
は整数論できわめて重要であるばかりでなく,その他の分野でも頻繁に登場する.彼らの素数定理の証明はこのリーマンの![]() 関数を本質的に用いる.1949年になってセルバーグ(A.Selberg)が
関数を本質的に用いる.1949年になってセルバーグ(A.Selberg)が![]() 関数を用いない初等的な方法で示した.これらについては『数論初歩』の範囲をこえる.
関数を用いない初等的な方法で示した.これらについては『数論初歩』の範囲をこえる.
青空学園では2005年〜2007年に数論の読者会をした.そこで『解析的整数論』(末綱恕一,岩波書店)に載っている素数定理の証明を紹介した.読書会に使った『数論I』の定理7.3 までは用いる.その他は出来るかぎり完結的に整理した.といっても,関数を中心に複素関数論を使うので,理解は難しい.それを以下に紹介する.
素数については今日もまだ未解決な問題がたくさんあることを指摘し本節を終えなければならない.それにしても,この世界に素数があるということはなんと不思議なことなのだろう.
素数定理の証明 いくつかの準備をして,素数定理を示す.1930年代のランダウらの方法である. 『数論I』p.266にあるように \[ \psi(x)\equiv \sum_{p^m\leqq x} \log p \] を考える.
補題
$s=\sigma+ti$ において $\sigma >1$ なら
\[
-\dfrac{\zeta'(s)}{\zeta(s)}
=s\int_1^{\infty}\dfrac{\psi(x)}{x^{s+1}}\,dx
=s\int_0^{\infty}\psi(e^u)e^{-us}\,du
\]
証明
チェビシフの定理より
\begin{eqnarray*}
\psi(x)
&=&\sum_{p\le x}\left[\dfrac{\log x}{\log p} \right]\log p
\le\sum_{p \le x}\dfrac{\log x}{\log p}\log p\\
&&\quad \quad =\pi(x)\log x=O(x)
\end{eqnarray*}
これから積分の存在することは確かである.
\[
-\log(1-u)=u+\dfrac{u^2}{2}+\dfrac{u^3}{3}+\cdots
\]
なので
\[
\log \zeta(s)=-\sum_p\log\left(1-\dfrac{1}{p^s} \right)
=\sum_{p,m}\dfrac{1}{mp^{ms}}
\]
この両辺を微分することにより
\begin{eqnarray*}
-\dfrac{\zeta'(s)}{\zeta(s)}&=&
\sum_{n=1}^{\infty}\dfrac{\psi(n)-\psi(n-1)}{n^s}=
\sum_{n=1}^{\infty}\psi(n)\left\{\dfrac{1}{n^s}-\dfrac{1}{(n+1)^s}\right\}\\
&=&\sum_{n=1}^{\infty}\psi(n)s\int_n^{n+1}\dfrac{dx}{x^{s+1}}
=s\sum_{n=1}^{\infty}\int_n^{n+1}\dfrac{\psi(x)}{x^{s+1}}\,dx\\
&=&s\int_1^{\infty}\dfrac{\psi(x)}{x^{s+1}}\,dx
\end{eqnarray*}
このなかで $x=e^u$ とおけば,第二の積分になる.□
補題
$v$ が0でない実数なら
\[
\dfrac{1}{2}\int_{-2}^2\left(1-\dfrac{|t|}{2} \right)e^{vti}\,dt
=\dfrac{\sin^2v}{v^2}
\]
証明
\begin{eqnarray*}
左辺&=&\dfrac{1}{2}\left\{\int_{-2}^0\left(1-\dfrac{|t|}{2} \right)e^{vti}\,dt
+\int_0^2\left(1-\dfrac{|t|}{2} \right)e^{vti}\,dt \right\}\\
&=&\dfrac{1}{2}\left\{\int_0^2\left(1-\dfrac{|t|}{2} \right)e^{-vti}\,dt
+\int_0^2\left(1-\dfrac{|t|}{2} \right)e^{vti}\,dt \right\}\\
&=&\int_0^2\left(1-\dfrac{t}{2} \right)\cos vt\,dt\\
&=&\left[\left(1-\dfrac{t}{2} \right)\dfrac{\sin vt}{v} \right]_0^2
+\int_0^2\dfrac{1}{2}\dfrac{\sin vt}{v}\,dt=\dfrac{1-\cos vt}{2v^2}
=右辺\quad □
\end{eqnarray*}
実数 $u$ に対し
\[
H(u)\equiv e^{-u}\psi(e^u)
\]
と書く.明らかに $y_2\geqq y_1$ のとき
\begin{equation}
H(y_2)\geqq H(y_1)e^{y_1-y_2}
\end{equation}
が成り立つ.
補題
$\lambda >0$ のとき任意の実数 $y$ に対し
\[
K(y,\ \lambda)=\int_{-\infty}^{\lambda y}H\left(y-\dfrac{v}{\lambda} \right)
\dfrac{\sin^2v}{v^2}\,dv
\]
が存在する.かつ
\[
\lim_{y \to \infty}K(y,\ \lambda)
\]
も存在し,$\displaystyle \int_{-\infty}^{\infty}\dfrac{\sin^2v}{v^2}\,dv$に一致する.
証明
\[
\int_0^{\infty}e^{-u(s-1)}\,du=\dfrac{1}{s-1}
\]
となるので,
補題より,
\[
\left(-\dfrac{\zeta'(s)}{\zeta(s)}-\dfrac{s}{s-1} \right)\dfrac{1}{s}
=\int_0^{\infty}\left\{H(u)-1\right\}e^{-u(s-1)}\,du
\]
$\lambda >0,\ \epsilon >0$ と実数 $y$ に対し
\begin{eqnarray*}
&&\int_{-2}^2\left(1-\dfrac{|t|}{2} \right)e^{\lambda yti}
\left\{-\dfrac{\zeta'(1+\epsilon+\lambda ti)}{\zeta(1+\epsilon+\lambda ti)}-\dfrac{1+\epsilon+\lambda ti}{\epsilon+\lambda ti} \right\}\dfrac{dt}{1+\epsilon+\lambda ti}\\
&&\quad =\int_{-2}^2\left(1-\dfrac{|t|}{2} \right)e^{\lambda yti}
\left\{\int_0^{\infty}\left\{H(u)-1\right\}e^{-\epsilon u}e^{-\lambda uti}\,du\right\}\,dt\\
&&\quad =\int_0^{\infty}\left\{H(u)-1\right\}e^{-\epsilon u}\,du
\int_{-2}^2\left(1-\dfrac{|t|}{2} \right)e^{\lambda (y-u)ti}\,dt\\
&&\quad =\dfrac{1}{\lambda}\int_{-\infty}^{\lambda y}\left\{H\left(y-\dfrac{v}{\lambda} \right)-1 \right\}e^{-\epsilon\left(y-\frac{v}{\lambda} \right)}\,dv
\int_{-2}^2\left(1-\dfrac{|t|}{2} \right)e^{vti}\,dt\\
&&\quad =\dfrac{2}{\lambda}\int_{-\infty}^{\lambda y}H\left(y-\dfrac{v}{\lambda} \right)e^{-\epsilon\left(y-\frac{v}{\lambda} \right)}\dfrac{\sin^2v}{v^2}\,dv
-\dfrac{2}{\lambda}\int_{-\infty}^{\lambda y}e^{-\epsilon\left(y-\frac{v}{\lambda} \right)}\dfrac{\sin^2v}{v^2}\,dv
\end{eqnarray*}
『数論I』定理7.3 より $s=1+ti\ (t\ne 0)$ で $\zeta(s)$ は零点をもたない.
したがって $\lambda\geqq 1$ となる範囲で
\[
\dfrac{\zeta'(s)}{\zeta(s)}+\dfrac{1}{s-1}
\]
は正則である.この結果 $\epsilon\to 0$ のとき,第1行の積分値の極限は存在する.
一方,最終行の第二の積分値の極限も存在する.
これらの極限では積分内で $\epsilon\to 0$ としてよい.
この結果,第一の積分についても同様であり.
\begin{eqnarray*}
&&K(y,\ \lambda)\\
&&=\dfrac{\lambda}{2}\int_{-2}^2\left(1-\dfrac{|t|}{2} \right)e^{\lambda yti}
\left\{-\dfrac{\zeta'(1+\lambda ti)}{\zeta(1+\lambda ti)}-\dfrac{1+\lambda ti}{\lambda ti} \right\}\dfrac{dt}{1+\lambda ti}+\int_{-\infty}^{\lambda y}\dfrac{\sin^2v}{v^2}\,dv
\end{eqnarray*}
が存在した.
右辺の第一の積分は,『数論I』定理7.3 より,ある連続関数を
フーリエ級数に展開した係数であるから $y\to \infty$ のときは0に収束する.
よって
\[
\lim_{y \to \infty}K(y,\ \lambda)=\int_{-\infty}^{\infty}\dfrac{\sin^2v}{v^2}\,dv
\]
(注)
この値は実は$\pi$になるが,有限確定値であること以外は次の定理では使わないので,
『解析的整数論』でも示されていない.
素数定理
\[
\pi(x)\sim\dfrac{x}{\log x}
\]
証明
第1段階として,
\[
\psi(x)\sim x\quad 即ち \quad\lim_{y\to \infty}H(y)=1
\]
を示す.
補題の積分値を $P$ とおく.
\[
P\equiv \lim_{y \to \infty}K(y,\ \lambda)=\int_{-\infty}^{\infty}\dfrac{\sin^2v}{v^2}\,dv
\]
このとき $\lambda >0$なので,補題と不等式より
\[
P \geqq \overline{\lim_{y \to \infty}}\int_{-\sqrt{\lambda}}^{\sqrt{\lambda}}
H\left(y-\dfrac{v}{\lambda} \right)\dfrac{\sin^2v}{v^2}\,dv
\geqq
\overline{\lim_{y \to \infty}}\int_{-\sqrt{\lambda}}^{\sqrt{\lambda}}
H\left(y-\dfrac{1}{\sqrt{\lambda}}\right)e^{-\frac{2}{\sqrt{\lambda}}}\dfrac{\sin^2v}{v^2}\,dv
\]
ゆえに
\[
\overline{\lim_{y \to \infty}}H(y)=
\overline{\lim_{y \to \infty}}H\left(y-\dfrac{1}{\sqrt{\lambda}}\right)\leqq
\dfrac{Pe^{\frac{2}{\sqrt{\lambda}}}}{\displaystyle \int_{-\sqrt{\lambda}}^{\sqrt{\lambda}}\dfrac{\sin^2v}{v^2}\,dv}
\]
最後の式は $\lambda\to \infty$ のとき1に収束するので,
\begin{equation}\label{siki2}
\overline{\lim_{y \to \infty}}H(y)\leqq 1
\end{equation}
不等式から $H(y)$ は有界である.
\[
H(y)\le Q
\]
とおく.再び補題と不等式より
\begin{eqnarray*}
P&=&\lim_{y \to \infty}\int_{-\infty}^{\lambda y}H\left(y-\dfrac{v}{\lambda} \right)
\dfrac{\sin^2v}{v^2}\,dv\\
&\leqq&
Q\int_{-\infty}^{-\sqrt{\lambda}}\dfrac{dv}{v^2}+
\lim_{\overline{y \to \infty}}
\int_{-\sqrt{\lambda}}^{\sqrt{\lambda}}
H\left(y+\dfrac{1}{\sqrt{\lambda}} \right)e^{\frac{2}{\sqrt{\lambda}}}
\dfrac{\sin^2v}{v^2}\,dv
+Q\int_{\sqrt{\lambda}}^{\infty}\dfrac{dv}{v^2}\\
&\leqq&
\dfrac{2Q}{\sqrt{\lambda}}+Pe^{\frac{2}{\sqrt{\lambda}}}
\lim_{\overline{y \to \infty}}H\left(y+\dfrac{1}{\sqrt{\lambda}} \right)
\end{eqnarray*}
つまり
\[
\lim_{\overline{y \to \infty}}H(y)\geqq e^{-\frac{2}{\sqrt{\lambda}}}
\left(1-\dfrac{2Q}{P\sqrt{\lambda}} \right)
\]
この右辺も $\lambda\to \infty$ のとき1に収束するので,
\begin{equation}
\lim_{\overline{y \to \infty}}H(y)\geqq 1
\end{equation}
2つの不等式から
\begin{equation}
\lim_{y \to \infty}H(y)=1
\end{equation}
が示された.
これをもとに素数定理を示す.$x >e$ に対して
\[
\omega=\dfrac{x}{\log^2 x}
\]
とおく.$\omega< x$である.
式から
\begin{eqnarray*}
\psi(x) &\leqq& \pi(x)\log x \leqq
\pi(\omega)\log x+\sum_{\omega< p\leqq x}\dfrac{\log p}{\log \omega}\log x \\
&\leqq& w\log x+\dfrac{\log x}{\log \omega}\psi(x)
\end{eqnarray*}
よって
\[
1
\leqq \dfrac{\pi(x)\log x}{\psi(x)}
\leqq \dfrac{x}{\psi(x)\log x}+\dfrac{\log x}{\log \omega}
\]
ここで等式から
\[
\lim_{x \to \infty}\dfrac{x}{\psi(x)}=1
\]
また
\[
\lim_{x \to \infty}\dfrac{\log x}{\log \omega}=
\lim_{x \to \infty}\dfrac{\log x}{\log x-2\log(\log x)}=1
\]
であるから
\[
\lim_{x \to \infty}\left(\dfrac{x}{\psi(x)\log x}+\dfrac{\log x}{\log \omega} \right)=1
\]
つまり,素数定理は示された.□