自然数の集合![]() を基礎に,整数の集合
を基礎に,整数の集合![]() と有理数の集合
と有理数の集合![]() を構成することができる.その道筋を考えよう.そのために,今後も必要になる集合の同値関係による類別を明確にしておく.これは後に整数の類別においても基礎的な概念となるものである.
を構成することができる.その道筋を考えよう.そのために,今後も必要になる集合の同値関係による類別を明確にしておく.これは後に整数の類別においても基礎的な概念となるものである.
この同値関係による商集合
![]() に和「+」と積「
に和「+」と積「![]() 」という二つの演算を定義する.
」という二つの演算を定義する.
![]() の二つの要素
の二つの要素
![]() をとる.
をとる.
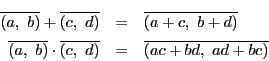
![]() をとったがこの類が
をとったがこの類が
![]() の他の要素
の他の要素![]() を用いて表されていたとする.このとき
を用いて表されていたとする.このとき
![]() であるが,こちらを用いて,
であるが,こちらを用いて,
![]() の和を作ると
の和を作ると
![]() となる.このとき,
となる.このとき,![]() と
と
![]() は同値である.実際
は同値である.実際![]() であるので
であるので
![]() が成り立つ.従って和は同じ類に属するいずれの要素を用いても同じ類を定める.このことを和は適切に定義されるという.積についても同様に確かめられる.さらに,
が成り立つ.従って和は同じ類に属するいずれの要素を用いても同じ類を定める.このことを和は適切に定義されるという.積についても同様に確かめられる.さらに,
![]() が和の単位元,
が和の単位元,
![]() が積の単位元,
が積の単位元,
![]() が
が
![]() 和に関する逆元であることが確認でき,これによって
和に関する逆元であることが確認でき,これによって
![]() が環をなすことが確認できる.
が環をなすことが確認できる.
この環を整数の集合(整数環)![]() いう.
いう.
![]() から
から
![]() への写像を自然数
への写像を自然数![]() を用いて
を用いて
自然数だけを用いて整数を構成しようとした.そのために自然数の組に
![]() のような
同値関係を入れ,同値なものを同一視したのである.
のような
同値関係を入れ,同値なものを同一視したのである.![]() が整数の
が整数の![]() に,
に,![]() が整数の
が整数の![]() になるわけである.
になるわけである.
![]() を整数の集合とする.次のような整数の組の集合を考える.
を整数の集合とする.次のような整数の組の集合を考える.
集合
![]() のこの関係での商集合
のこの関係での商集合
![]() に和「+」と積「
に和「+」と積「![]() 」を定める.
」を定める.
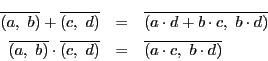
これは適切に定義される.例えば和についていえば
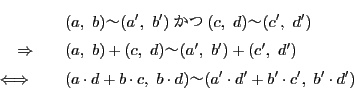
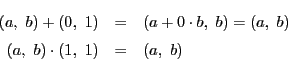
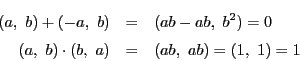
この体をを有理数体![]() という.
という.
さらに
以下,有理数体の積で文字の場合,積の記号![]() は約すか
または紛らわしくなるときは
は約すか
または紛らわしくなるときは![]() で書こう.
で書こう.
こうして自然数の集合![]() ,整数環
,整数環![]() ,有理数体
,有理数体![]() が順次構成されるのである.
が順次構成されるのである.