次: ピタゴラス数の一般形 上: 素数 前: 素数

素数の定義と素因数分解

0および$\pm 1$でない整数$a$は少なくとも$\pm 1$と$\pm a$を約数に持つ． $\pm 1$および $\pm a$ 以外の約数を「真の約数」ともいう．

定義 4        真の約数を持たない1より大きい正の整数$a$を 素数 という． これに対して真の約数を持つ整数を 合成数 という．

整数$\alpha$をこれ以上分解できないところまで分解して，

$$\alpha=\pm {p_1}^{e_1}{p_2}^{e_2}\cdots{p_m}^{e_m}$$

の形にしたものを素因数分解という．

$p_1,\ p_2,\ \cdots,\ p_m$は異なる素数， $e_1,\ e_2,\ \cdots,\ e_m$は正の整数である． どのような整数も，因数分解できしかも順序を除けばただ一通りである．

例えば，48をどんな順で因数分解しても，素因数分解までいけば(順序以外は)同じである．

$$\begin{eqnarray*} &&48=2^2\cdot12=2^2\cdot2^2\cdot3=2^4\cdot3\\ &&48=3\cdot18=3\cdot2^4 \end{eqnarray*}$$

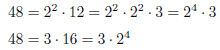
このことは次のようにまとめられる．この定理は算術の基本定理ともいわれる． 高校数学ではこれは証明なしに認めてよい．

定理 4        合成数を素数の積に分解することができる． かつ，その分解の結果は因数の順序をのぞけば一通り(これを一意という)である．

証明      数学的帰納法で示す．

(1)     最小の合成数は$4$で $4=2\times 2$ でありこれ以外にないから，成立．

(2)     $a$ よりも小さい(正の)整数については定理が成立していると仮定する．

$a$の分解の可能性を示す． $a$ は合成数であるから

$$a=b\times c\quad (1<b<a,\ 1<c<a)$$

と分解される．数学的帰納法の仮定により $b$ も $c$ も素数の積に分解されるので， $a$ も素数の積に分解される．

$a$の分解の一意性を示す． $a$ を素因数に分解して二つの分解

$$a=p_1p_2\cdots p_m=q_1q_2\cdots q_n$$

を得たとする．定理2の(4)より，二つの整数の積が素数 $p$ の倍数なら， 因数のなかの少なくとも一つがその素数の倍数である．三つ以上の数以上の積の場合も $abc=(ab)c$ のように括弧でくくり順次考えれば，いずれかが $p$ の倍数になる．したがって， $p_1,\ p_2,\ \cdots,\ p_m$ のいずれかは $q_1$ の倍数である．いま $p_1$ が $q_1$ の倍数であるとすれば, $p_1$ は素数なので, $p_1=q_1$ である．

$$∴\quad p_2\cdots p_m=q_2\cdots q_n$$

この両辺の数を $b$ とすれば $b<a$ なので数学的帰納法の仮定からこの分解は順序を除いて一意である． よって$a$において定理が成立する．

(3)     (1)(2)より，任意の整数に対して定理が成立することが示された． (証明終わり)

例 2        素因数分解が一通りであること用いた証明の例をあげよう． 次の(1)と(2)を証明しよう．

(1)は先の入試問題1の解答では，具体的に書いて済ませたところである． これを一般的に示すときには以下のようにしなければならない． また(2)は，高校数学の教科書に書いてある方法とは異なるものである． それぞれ次のように素因数分解の一意性を根拠に示される．

(1)

$a$と$b$を整数，$p$を素数とする．$ab$が$p$の倍数ならば，$a$または$b$が$p$の倍数である．

(2)

$\sqrt{2}$は有理数ではない．

(1)

$ a $ が $ p $ で割り切れないとする． つまり $ a $ と $ p $ は互いに素であるとする． $ ab $ が $ p $ の倍数であるから，定理2の(4)によって， $ b $ は $ p $ の倍数である．
$ b $ が $ p $ で割り切れないときは $ a $が $ p $ の倍数になる． (証明終わり)

(2)

有理数であるとし， $\sqrt{2}=\dfrac{n}{m}$とおく．これから

$$2m^2=n^2$$

右辺$n^2$の因数分解のなかに素因数2は偶数個ある． 左辺$2m^2$の因数分解のなかに素因数2は奇数個ある． これは素因数分解の一意性と矛盾する． よって$\sqrt{2}$は有理数ではない．(証明終わり)

定理 5        素数の数は無限である．

証明      背理法で示す．素数の個数が有限であると仮定する．その個数を $n$ 個とし， $p_1,\ p_2,\ \cdots,\ p_n$ をすべての素数とする． このとき

$$a=p_1p_2\cdots p_n+1$$

とおく． 定理4 より$a$は素数の積に分解される．

一方$a$は $p_1,\ p_2,\ \cdots,\ p_n$ のいずれで割っても1余る． つまり， $p_1,\ p_2,\ \cdots,\ p_n$ は$a$の約数でない． よって$a$ の素因数分解に現れる素数は $p_1,\ p_2,\ \cdots,\ p_n$ ではあり得ず， それら以外の素数である． これは $p_1,\ p_2,\ \cdots,\ p_n$ がすべての素数という仮定と矛盾する． ゆえに素数の数は無限である． (証明終わり)

人類史上はじめて背理法を用いて素数が無数にあることを示したのもまたエウクレイデスである． これと同じ内容の論証が『原論』に書かれている．

次: ピタゴラス数の一般形 上: 素数 前: 素数