![]() の最大公約数が1である組の一般形を求めてみよう.
の最大公約数が1である組の一般形を求めてみよう.
![]() がともに偶数なら
がともに偶数なら![]() も偶数になって,
最大公約数が1でなくなるので,
も偶数になって,
最大公約数が1でなくなるので,![]() と
と![]() のいずれかは奇数である.
のいずれかは奇数である.
![]() を偶数とする.
を偶数とする. ![]() と
と ![]() は奇数になる.
は奇数になる.
さらに,
![]() の左辺を素因数分解すると,
各素因数は偶数個現れる.
の左辺を素因数分解すると,
各素因数は偶数個現れる.
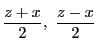 が互いに素なので,
これらの素因数はそれぞれ
が互いに素なので,
これらの素因数はそれぞれ
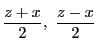 のいずれか一方にのみ現れ,
その結果
のいずれか一方にのみ現れ,
その結果
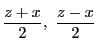 の素因数分解で
各素因数はすべて偶数個現れる.
の素因数分解で
各素因数はすべて偶数個現れる.
よって
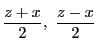 はいずれも平方数である.
はいずれも平方数である.
最大公約数が1であるための ![]() と
と ![]() の条件を求める.
の条件を求める.
![]() と
と ![]() はたがいに素で
はたがいに素で ![]() ,さらに
,さらに ![]() が奇数なので
が奇数なので
![]() と
と ![]() の偶数奇数が異なることが,
の偶数奇数が異なることが, ![]() の最大公約数が1であるために必要である.
の最大公約数が1であるために必要である.
よって,最大公約数が1の解は
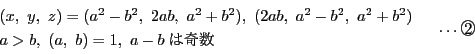
逆に条件![]() を満たす
を満たす ![]() と
と ![]() を用いて上のいずれかで
表される
を用いて上のいずれかで
表される ![]() は最大公約数が1の解である.
は最大公約数が1の解である.
それを示す.
![]() のように定まる
のように定まる![]() がピタゴラス数であることは明か.
がピタゴラス数であることは明か.
もしこの ![]() に共通素因数
に共通素因数 ![]() があるとする.
があるとする.
すると ![]() か
か ![]() を考えると
を考えると ![]() は
は
ところが ![]() が
が ![]() 約数なので
約数なので
![]() が偶数.
が偶数.
これは条件 ![]() は奇数 に反する.
よって確かに
は奇数 に反する.
よって確かに![]() で定まる
で定まる![]() は,
最大公約数が1のピタゴラス数である.
は,
最大公約数が1のピタゴラス数である.
必要条件とあわせて,![]() で表される
で表される![]() が最大公約数が1の
ピタゴラス数のすべてである.
が最大公約数が1の
ピタゴラス数のすべてである.