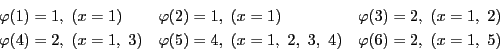
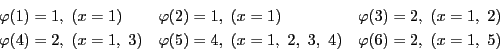
入試問題21のように,オイラーの関数を題材とする問題がある.まずこれを解いてみよう.
この問題の(2)の解は異なる素数![]() と
と![]() に対して
に対して
![]() が成り立つことを意味している.
一般的に次のことが成り立つ.
が成り立つことを意味している.
一般的に次のことが成り立つ.
証明
![]() とし,
とし,
![]() を
1以上
を
1以上![]() 以下で
以下で![]() と互いに素な整数とする.
と互いに素な整数とする.
![]() とし,
とし,
![]() もまた同様に選ばれているとする.
もまた同様に選ばれているとする.
![]() の組は
の組は
![]() 個ある.その一つをとる.
個ある.その一つをとる.
![]() と
と![]() が互いに素なので
が互いに素なので
この式の値を![]() で割った余りを
で割った余りを![]() とする.
とする.
![]() は
は
![]() を
を![]() に変え同様にして
に変え同様にして![]() をとる.
をとる.
![]() ,
,
![]() より
より![]() と
と![]() は
は![]() を法として合同でない.
よって
を法として合同でない.
よって![]() を法として合同でない.
を法として合同でない.
![]() が異なる場合も,両方異なる場合も同様である.
が異なる場合も,両方異なる場合も同様である.
![]() と互いに素で互いに合同でない整数が少なくとも
と互いに素で互いに合同でない整数が少なくとも
![]() 個存在した.つまり
個存在した.つまり
逆に
![]() とすると,
とすると,![]() が
が![]() とも
とも![]() とも互いに素なので
とも互いに素なので
![]() を法として
を法として![]() に,
に, ![]() を法として
を法として![]() に合同となる
に合同となる![]() が存在する.
が存在する.
![]() と
と![]() が
が![]() に関して合同でなければ
に関して合同でなければ
![]() または
または![]() の少なくとも一方に関しても合同でない.
よって異なる
の少なくとも一方に関しても合同でない.
よって異なる![]() に対する
に対する
![]() の組はすべて異なる.
の組はすべて異なる.
あわせて等号が成立し定理が示された. (証明終わり)
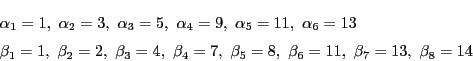
![]() をとってみよう.
をとってみよう.
そして![]() と
と![]() については
については![]() は
は![]() の倍数ではないので
の倍数ではないので
![]() を法として合同でない.
を法として合同でない.
このようにして得られる![]() 個の
個の![]() が
1以上210以下で210と互いに素な数の全体となる.
が
1以上210以下で210と互いに素な数の全体となる.