![]() を自然数とするとき,
を自然数とするとき,![]() で
で![]() と
と![]() の最大公約数が1となる自然数
の最大公約数が1となる自然数![]() の個数を
の個数を![]() とする.
とする.
- (1)
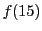 を求めよ.
を求めよ.
- (2)
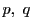 を互いに素な素数とする.このとき
を互いに素な素数とする.このとき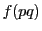 を求めよ.
を求めよ.
- (3)
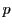 を素数,
を素数,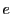 を自然数とする.このとき
を自然数とする.このとき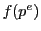 を求めよ.
を求めよ.
![]() を自然数とするとき,
を自然数とするとき,![]() で
で![]() と
と![]() の最大公約数が1となる自然数
の最大公約数が1となる自然数![]() の個数を
の個数を![]() とする.
とする.
![]() を自然数とし,
を自然数とし,![]() を
を![]() より小さくかつ
より小さくかつ![]() と互いに素な自然数の総数とする.すなわち
と互いに素な自然数の総数とする.すなわち
である.このとき以下の問いに答えよ.
ただし,必要に応じて以下の数表を使つてもよい.
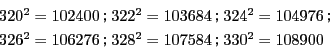
自然数 ![]() の関数
の関数 ![]() を
を
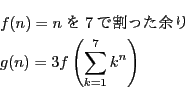
![]() を素数,
を素数,![]() を
を![]() で割り切れない自然数とし,1から
で割り切れない自然数とし,1から![]() までの自然数の集合を
までの自然数の集合を![]() とおく.
とおく.
![]() は素数,
は素数,![]() は正の整数とする.以下の問いに答えよ.
は正の整数とする.以下の問いに答えよ.