

 次: 演習問題
上: フェルマの小定理
前: オイラーの関数
次: 演習問題
上: フェルマの小定理
前: オイラーの関数
定理 14
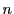
を正整数,
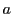
を
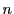
と互いに素な整数とする.
このとき次式が成り立つ.
証明
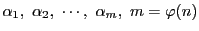 を
を
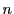 と互いに素で,相互に
と互いに素で,相互に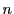 を法として合同でない整数とする.
を法として合同でない整数とする.
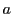 が
が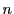 と互いに素なので,
と互いに素なので,
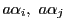 が
が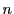 に関して合同になるのは
に関して合同になるのは
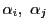 が合同なときにかぎる.よって
が合同なときにかぎる.よって
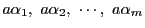 は
は
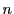 と互いに素でかつ互いに合同でない整数である.
と互いに素でかつ互いに合同でない整数である.
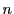 と互いに素でかつ互いに合同でない整数の個数が
と互いに素でかつ互いに合同でない整数の個数が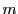 なので,
なので,
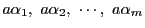 のそれぞれは
のそれぞれは
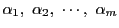 のそれぞれ1つずつと
のそれぞれ1つずつと
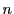 を法として合同である.よってその積は
を法として合同である.よってその積は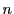 を法として互いに合同である.
を法として互いに合同である.
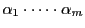 は
は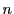 と互いに素なので,
と互いに素なので,
である.
(証明終わり)
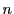 が素数のときは
が素数のときは
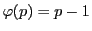 .したがって
.したがって
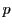 と互いに素な
と互いに素な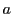 に対して
に対して
である.これをフェルマの小定理という.
これをそのまま入試問題としたものもある.
また,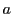 が
が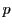 と互いに素であるという条件をとり,任意の整数
と互いに素であるという条件をとり,任意の整数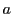 とすると,
とすると,
が成り立つ.
Aozora
2015-03-02
![]() と互いに素でかつ互いに合同でない整数の個数が
と互いに素でかつ互いに合同でない整数の個数が![]() なので,
なので,
![]() のそれぞれは
のそれぞれは
![]() のそれぞれ1つずつと
のそれぞれ1つずつと
![]() を法として合同である.よってその積は
を法として合同である.よってその積は![]() を法として互いに合同である.
を法として互いに合同である.
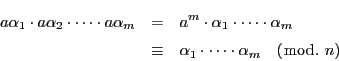
![]() が素数のときは
が素数のときは
![]() .したがって
.したがって
![]() と互いに素な
と互いに素な![]() に対して
に対して
![]() が
が![]() と互いに素であるという条件をとり,任意の整数
と互いに素であるという条件をとり,任意の整数![]() とすると,
とすると,