- (1)
- 15と互いに素な15以下の数は
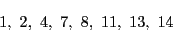
である.よって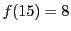 .
.
- (2)
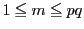 の範囲にある
の範囲にある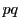 と互いに素でない数は
と互いに素でない数は
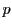 の倍数と
の倍数と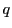 の倍数でありそれぞれ,
の倍数でありそれぞれ,
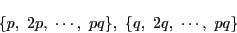
である.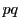 が共通なので,互いに素でない数が
が共通なので,互いに素でない数が
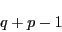
よって
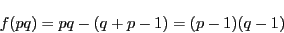
- (3)
- 1から
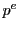 までの数のなかで
までの数のなかで 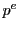 と互いに素では ないものは,
と互いに素では ないものは,
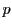 で割り切れるものに他ならず,それは
で割り切れるものに他ならず,それは
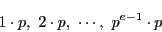
の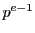 個だけある.よって
個だけある.よって
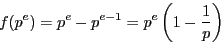
である.
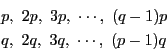
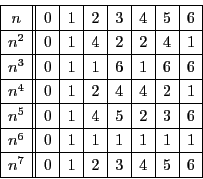
他の演習問題にあるように,![]() が7の倍数になることを
が7の倍数になることを![]() に関する数学的帰納法で示すことができる.
に関する数学的帰納法で示すことができる.
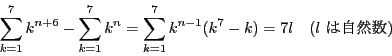
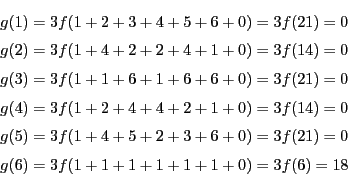
よって![]() は
は![]() 個の要素からなり,
個の要素からなり,
![]() の要素の個数と一致する.よって
の要素の個数と一致する.よって
![]() である.
である.
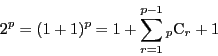
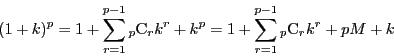
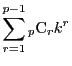 は
は
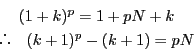
つまり, ![]() を
を ![]() で割った余りは
で割った余りは ![]() を
を ![]() で割った余りである.
で割った余りである.
![]() は
は
![]() をそれぞれ
をそれぞれ
![]() 個ずつを並べる場合の数である.
その一つの並べ方に対して,
個ずつを並べる場合の数である.
その一つの並べ方に対して,
![]() 個ずつある
個ずつある
![]() の一つ一つを区別すると
の一つ一つを区別すると
![]() 個でき,それらの並べ方の総数が
個でき,それらの並べ方の総数が![]() である.よって
である.よって
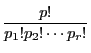 は
は
式