(1) 余りは
![]() にある.よって
にある.よって
よって
(2) 同様に
これから![]() .
また
.
また![]() とおけ,
とおけ,![]() なので
なので
![]() である.あわせて
である.あわせて
である.8と7は互いに素なので
(1) $a,\ b$がいずれも3の倍数でないとする.
$a$と$b$を3で割った商を$q_1,\ q_2$,余りを$r_1,\ r_2$とする.
$r_1,\ r_2=1,\ 2$である.
\[
a=3q_1+r_1,\
b=3q_2+r_2
\]
このとき
\[
ab=3(3q_1q_2+q_1r_2+q_2r_1)+r_1r_2
\]
$r_1r_2=1,\ 2,\ 4$であるから,$ab$は3の倍数ではない.
$ab$が3の倍数であるという仮定に矛盾した.
よって$a$と$b$はともに3の倍数である.
(2) (1)から$a$か$b$が3の倍数である.$a$が3の倍数とする.
$a+b$が3の倍数で$a$が3の倍数なので,その差である$b$も3の倍数である.
$b$が3の倍数であるときも同様であり,$a$と$b$はともに3の倍数であることが示された.
(3) $a^2+b^2=(a+b)^2-2ab$であるから,この数と$a+b$が3の倍数なら,
$2ab$が3の倍数である.2と3は互いに素なので$ab$が3の倍数となり,
(1)から$a$と$b$はともに3の倍数である.
(0) $mn$は$p$の倍数なので,$mn$の素因数分解に$p$が現れる.
$m$も$n$も$p$の倍数でなければ,積$mn$の素因数分解に$p$は現れない.
これは素真数分解の一意性(3節定理4)と矛盾する.
よって,$m$または$n$は$p$の倍数である.
(1) $ab$が$p$の倍数なので$a$か$b$のいずれかが$p$の倍数である.
$a$が$p$の倍数とし,$a=pa'$とおく.$a+b$が$p$の倍数なのでこれを$pN$とおく.
このとき
\[
b=(a+b)-a=pN-pa'
\]
となり$b$は$p$の倍数である.
$b$が$p$の倍数のときも同様に$a$が$p$の倍数となる.
よって$a$と$b$はともに$p$の倍数である.
(2) $a^2+b^2=(a+b)^2-2ab$であるから,この数と$a+b$が$p$の倍数なら,
$2ab$が$p$の倍数である.$p$は奇素数なので2とは互いに素である.
よって$ab$が$p$の倍数となり,(1)から$a$と$b$はともに$p$の倍数である.
(3) $a^3+b^3=(a+b)(a^2-ab+b^2)$であるから,
$a+b$か$a^2-ab+b^2$の少なくとも一方は$p$の倍数である.
$a+b$が$p$の倍数のとき,$a^2+b^2$が$p$の倍数なので(2)によって$a$と$b$はともに$p$の倍数である.
$a^2-ab+b^2$が$p$の倍数のとき,$a^2+b^2$が$p$の倍数なので,$ab$が$p$の倍数である.
$a$が$p$の倍数とすると$a^2+b^2$が$p$の倍数であることから$b^2$が$p$の倍数である.
$p$は素数なので$b$が$p$の倍数である.はじめに$b$が$p$の倍数であるときも同様である.
よって$a$と$b$はともに$p$の倍数であることが示された.
別解
\[
a^3+b^3=(a+b)(a^2+b^2)-ab(a+b)
\]
であるから,$ab(a+b)$が$p$の倍数になる.
$a+b$が$p$の倍数なら(2)より$a,\ b$が$p$の倍数.
$ab$が$p$の倍数なら$a^2b^2$も$p$の倍数なので,(1)から$a^2$と$b^2$が$p$の倍数.
$p$は素数なので,$a$と$b$が$p$の倍数.
(4) $a$が$p$の倍数なら,$a^n+b^n$が$p$の倍数であることから$b^n$も$p$の倍数.
$p$が素数でであるから,$b$も$p$の倍数である.逆の場合も同様.
そこで$a$も$b$も$p$の倍数あるか,両方とも$p$の倍数でないかのいずれかである.
$a$も$b$も$p$の倍数でないとする.
$n\ge 2$のとき,
\[
a^{n+1}+b^{n+1}=(a+b)(a^n+b^n)-ab(a^{n-1}+b^{n-1})
\]
であるから,このとき$a^{n-1}+b^{n-1}$が$p$の倍数になる.
くりかえし用いることにより,$a+b$と$a^2+b^2$がともに$p$の倍数になる.
このとき(2)から$a,\ b$が$p$の倍数になり,$a$も$b$も$p$の倍数でないという仮定と矛盾する.
よって$a$も$b$も$p$の倍数あることが示された.
(1) 余りは
![]() にある.よって
にある.よって
これから![]() .
また
.
また![]() とおけ,
とおけ,![]() なので
なので
![]() である.あわせて
である.あわせて
これから
さらに![]() と
と![]() の公約数は
の公約数は
![]() より,
1しかない.よって
より,
1しかない.よって
![]() は互いに素である.
は互いに素である.
![]() が
が![]() や
や![]() と1より大きい公約数をもてば,
と1より大きい公約数をもてば,
![]() が
が![]() や
や![]() と1より大きい公約数をもつ.
と1より大きい公約数をもつ.
![]() は互いに素なので,これはあり得ない.
よって,三つの自然数
は互いに素なので,これはあり得ない.
よって,三つの自然数![]() は互いに素である.
は互いに素である.
これは任意の奇数![]() に対して成立する.
奇数は無数にあるので,
三つの互いに素な自然数を三辺の長さとする直角三角形
が無数にあることが示された.
に対して成立する.
奇数は無数にあるので,
三つの互いに素な自然数を三辺の長さとする直角三角形
が無数にあることが示された.
任意に奇数を選ぶ.![]() としてみよう.
としてみよう.
しかし,これですべてのピタゴラス数が作れるわけではない.

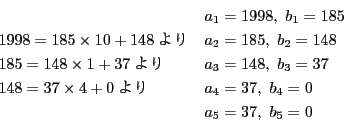
![]() を
を![]() で割った商を
で割った商を![]() とおくと,
とおくと,
![]() とかける. これから
とかける. これから![]() と
と ![]() の公約数は
の公約数は ![]() の
約数になり,
の
約数になり,![]() と
と![]() の公約数である.
の公約数である.
![]() と
と![]() の公約数で最大のものが最大公約数
の公約数で最大のものが最大公約数
![]() である.
ゆえに
である.
ゆえに
![]() .
また
.
また![]() と
と ![]() の公約数は
の公約数は ![]() の約数になる.
同様に考え
の約数になる.
同様に考え
![]() である.
である.