next up previous 次： 複素数の構成(一) 上： 複素数の構成 前： 教科書の定義

体

そこで聞きたいのだが，数とは何か．

史織　 「数」ですか．

南海　 「数」と名のつくものはどんなものがあるか．

史織　 まず，自然数，それから負の数，自然数と0と負の数をあわせて整数．

有理数，無理数，それから有理数と無理数をあわせて実数．

南海　 これはいずれも集合である．それら「数」の集合の特徴は．

史織　 足し算，かけ算ができる．引き算は，自然数だと $2-5$ はもう自然数ではない． 自然数の集合には属さない． 逆にこれらの引き算でできる数まであわせた集合が整数といえる．

割り算，整数を整数で割ると整数の集合には属さないものが出る．それらをあわせた集合が有理数．

南海　 先にあげてくれたような具体的な数の集合の特徴として，四則演算が定義されるということがある． その演算の結果が再びもとの集合に属したりしなかったりする．

有理数と実数は四則演算の結果が再び有理数か実数である．ある集合である演算ができ， さらにその演算の結果がその集合に属するとき，その集合はその演算に関して「閉じている」 という．

そこで，四則演算で閉じている集合 $K$ を考え，これを体と呼ぼう． 実際には次のように体であるための条件が整理される．

以下集合 $K$ を考え， $a$ や $b$ で $K$ の任意の要素を表す． 集合 $K$ が次の条件を満たすとき，「体」という．

  1. 2つの演算，加法$+$と乗法$\times$が定義されている． つまり，$K$ の要素 $a+b,\ a\times b$がそれぞれ確定する．
  2. 2つの演算は結合法則を満たす．

    \begin{displaymath} (a+b)+c=a+(b+c)\ ,\ \ (a\times b)\times c=a\times(b\times c) \end{displaymath}

  3. 加法は可換である．$a+b=b+a$が成り立つ．
  4. $a+e=a$， $a\times f=f\times a=a$ となる要素 $e$ と $f$ が存在する． $e$ を加法の単位元といい，通常0と書く．$f$ を乗法の単位元といい，通常1と書く．
  5. $a+x=0$となる$x$ が存在する． これを $a$ の加法の逆元といい，$-a$ と書く．
  6. 0でない要素$a$に対して$a\times x=1$となる$x$ が存在する． これを $a$ の乗法の逆元といい，$a^{-1}$ と書く．
  7. 加法と乗法について分配法則が成り立つ．

    \begin{displaymath} a\times(b+c)=a\times b+a\times c\ ,\ \ (b+c)\times a=b \times a+c \times a \end{displaymath}

乗法についても可換 $a\times b=b \times a$ が成り立つものを「可換体」と呼ぶ． 実際には可換体しか考えないのだが，行列の積のように「積」には可換でないものも 高校数学で出てくるので，体の定義も一般的にしておいた．

史織　 えーっと，体とは，要するに加法と乗法があって，加法も乗法も逆元がなければならないのだから 自然数や整数はだめで，体になっているのは上にいわれた有理数の集合．それから実数の集合…， でもこれだけしか思い浮かびません．他にないのですか．

南海　 いっぱいある．その例を練習問題にしよう． その前に今後よく使うので有理数の集合を $Q$ ，実数の集合を $R$ と書くことにする．

史織　 四則について閉じているといいますが， 体の定義には引き算や割り算の定義はありません．それはどうなるのですか．

南海　 可換体でないと複雜になるので，体は可換体，つまり乗法が交換可能であるとする． このとき

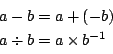
\begin{displaymath} \begin{array}{l} a-b=a+(-b)\\ a\div b=a\times b^{-1} \end{array}\end{displaymath}

で，減法，除法を定める．

逆元との和や積なので，減法，除法の結果も $K$ に属する．

史織　 そうか，わかりました．加法と乗法での逆元の存在が，四則演算で閉じていることを 示しているのですね．

南海　 さて，有理数を含み，実数に含まれる体の例として

\begin{displaymath} A=\{a+b\sqrt{2}\ \vert\ a,\ b \in Q \ \} \end{displaymath}

がある．その確認などを練習問題とする．

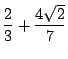史織　 $\dfrac{2}{3}+\dfrac{4\sqrt{2}}{7}$ のような形をした数の集合ですね．

演習 1       解答1

次の集合が体であることを示せ．ただし，実数が体であることは用いてよい．


  1. \begin{displaymath} A=\{a+b\sqrt{2}\ \vert\ a,\ b \in Q \ \} \end{displaymath}


  2. \begin{displaymath} B=\{a+b\sqrt{2}+c\sqrt{3}+d\sqrt{6}\ \vert\ a,\ b,\ c,\ d \in Q \ \} \end{displaymath}

南海　 体の例としてはその他に $x$ を変数とする有理式全体の集合がある．これを普通は $R(x)$ と書く．

\begin{displaymath} R(x)=\left\{\dfrac{f(x)}{g(x)}\biggl\vert f(x),\ g(x) は x の多項式 \right\} \end{displaymath}


Aozora Gakuen