次： 複素数の構成(その他) 上： 複素数の構成 前： 体

複素数の構成(一)

南海　 そこで，平面ベクトル，あるいは同じことだが， 平面上の座標 $(x,\ y)$ からはじめて，これを体にしようということなのだ．

史織　 でもベクトルなら加法はすでにありますね．

南海　 そうだ．しかしそれも改めて確認しよう． まず集合をはっきりさせなければならない．集合 $V$ を

$$V=\{(a,\ b)\ \vert\ a,\ b \in R\ \}$$

とする．実数の集合2つの直積ということだからこの $V$ はまた $R^2$ とも書かれる．

まずこの集合 $V$ の加法を次のように定める．

$$(a,\ b)+(c,\ d)=(a+c,\ b+d)$$

このとき，加法の単位元と逆元は?

史織　 ベクトルと同じですから単位元は $(0,\ 0)$ で $(a,\ b)$ の逆元は $(-a,\ -b)$ です．

南海　 では乗法をどのように定めるかだが，それは最初の

$$(a+bi)\times(c+di)=(ac-bd)+(ad+bc)i$$

を参考にすればよい．

史織　

$$(a,\ b)\times (c,\ d)=(ac-bd,\ ad+bc)$$

とさだめるのですね．

演習 2       解答2

この2つの演算 $+,\ \times$ によって $V$ は体にあることを確認せよ．

南海　 すべての条件を点検するのは結構面倒だが，複素数の計算を参考にしながらやればできる． 成分で見れば， $V$ と $C$ の加法と乗法が同じ演算になっていることがわかるはずだ．

これで平面上の点の集合が体になった．

ところで $V$ の要素で $(a,\ 0)$ という形をしたものからなる部分集合を考える．

$$\begin{eqnarray*} (a,\ 0)+(b,\ 0)&=&(a+b,\ 0)\\ (a,\ 0)\times(b,\ 0)&=&(ab-0,\ a\cdot 0+0\cdot b) =(ab,\ 0) \end{eqnarray*}$$

になるので，第一の成分について見れば実数の四則と同じになり，第二成分は常に0． したがってこのような要素の全体も体の定義を満たす．体 $V$ の部分集合でそれ自身体なので $V$ の部分体という．

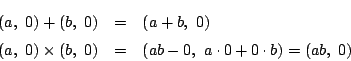
史織　 これって，複素平面の実数軸と同じではありませんか．

南海　 その通りなのだ．これが複素数の部分体である実数の集合 $R$ に対応するものだ．

このとき

$$(a,\ 0)\times(b,\ c)=(ab-0\cdot c,\ ac+0\cdot b) =(ab,\ ac)$$

であるから，$(a,\ 0)$と$(b,\ c)$の積は，ベクトルの実数倍と同じになっている．

また

$$(a,\ b)=(a,\ 0)\times(1,\ 0)+(b,\ 0)\times(0,\ 1)$$

と表すことができる．

ところでこの $(0,\ 1)$ だが $(0,\ 1)\times(0,\ 1)$はいくらか．

史織　

$$(0,\ 1)\times(0,\ 1)=(0\cdot 0-1\cdot 1,\ 0\cdot 1+1\cdot 0) =(-1,\ 0)=-1$$

です．

南海　 したがって$V$ は，実数 $R$ と同じものを含み， かつ2乗すると $-1$ になる要素が存在する体である． このような体が実際に構成された．

次にこの $V$ と 教科書で作られた$C$ が，実質的に同じもの(体として同型)であることを示そう．

集合 $V$ から複素数の集合 $C$ への写像

$$f\ :\ V\ \to \ C$$

を

$$f((a,\ b))=a+bi$$

で定める．これは明らかに一対一写像で， $V$ の演算の定義と $C$ の計算法則から， 加法や乗法の演算の結果も $f$ で対応する．

つまり

$$\begin{eqnarray*} f((a,\ b)+(c,\ d))=(a+bi)+(c+di)\\ f((a,\ b)\times(c,\ d))=(a+bi)\times(c+di) \end{eqnarray*}$$

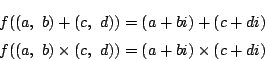
一対一写像があって演算もこのように対応するとき二つの集合は「体として同型」であるという． このとき二つの体は同一視できる． $V$ と $C$ は同型なのだ．

$(a,\ 0)$ の形をした要素からなる $V$ の部分集合は，この写像でちょうど $C$ の 部分集合である実数 $R$ に対応する．

$i$ はあるのかないのかわからないが $C$ と同じ型の具体的なモデルが構成できた．

最後に， 「『平方すると $-1$ になる数』は $\pm$ と二つあるはずなのに，どちらをとってもいいのか」 という質問に関していえば，先の同型写像 $f$ のかわりに

$$f((a,\ -b))=a+bi$$

としても，やはり一対一同型になるのだ．だからどちらを $i$ にしても， 同じものができると考えてよい．

ここで座標から複素数を構成する方法に関係する入試問題を一つ紹介する．

演習 3       ［90東京女子大］解答3

座標平面上の2点 $\mathrm{X}(x_1,x_2),\ \,\mathrm{Y}(y_1,y_2)$ に対し， 座標が $(x_1y_1-x_2y_2,\ x_1y_2+x_2y_1)$ である点を記号 $\mathrm{X} \circ \mathrm{Y}$ で表す．このとき，次の問いに答えよ．

1. 原点以外の2点 $\mathrm{A}(a_1,a_2),\ \mathrm{B}(b_1,b_2)$ に対し， $\mathrm{A}\circ\mathrm{X}=\mathrm{B}$ なる点 $\mathrm{X}$および $\mathrm{A}\circ\mathrm{Z}=\mathrm{A}$となる点 $\mathrm{Z}$の座標を求めよ．
2. 原点以外の相異なる3点 $\mathrm{P,Q,R}$ よりなる集合を$\mathrm{M}$とする． $\mathrm{M}$ のどの点 $\mathrm{X}$ に対しても $\mathrm{X \circ P},\ \mathrm{X \circ Q},\ \mathrm{X \circ R}$ がいずれも $\mathrm{M}$ の点であれば，点 $(1,0)$ は集合 $\mathrm{M}$ に属することを示せ．
3. (2)の条件がみたされるとき，$\mathrm{P}$の座標が$(1,0)$ であるとする． このとき， $\mathrm{Q \circ R}=\mathrm{P}$, $\mathrm{Q \circ Q}=\mathrm{R}$ となることを示せ．
4. $\mathrm{Q,\ R}$ の座標を求めよ．

南海　 この(2)(3)は結構難しい．複素数平面が高校数学になかったときの出題だ．

次： 複素数の構成(その他) 上： 複素数の構成 前： 体